Long post incoming
I’ve now added CAPS 2017. I’m not going to announce every addition, but I thought this one is worth mentioning, because with EricF and Shax both using the Blue starter in that tournament, we now have data, however scant, for all of the starter decks! Nothing for Bashing, though.
Let’s do a proper update.
Model structure
What’s the model currently accounting for?
- First-player (dis)advantage
- Player skill, which can be affected by whether they’re player 1 or 2
- Starter deck strength, affected by player position
- Spec strength, affected by player position
What’s it not accounting for?
- Player skill changing over time
- Synergies, or lack of, between specs and starters - all four parts of a deck are considered in isolation
- Effect on player skill of opponent, deck used (e.g. familiarity with their deck
- Effect on deck strength of opposing deck
Of these, the starter/spec interactions are probably going to have the biggest effect, so I’ll be adding that next time.
Prior choice: what do model predictions look like before adding data?
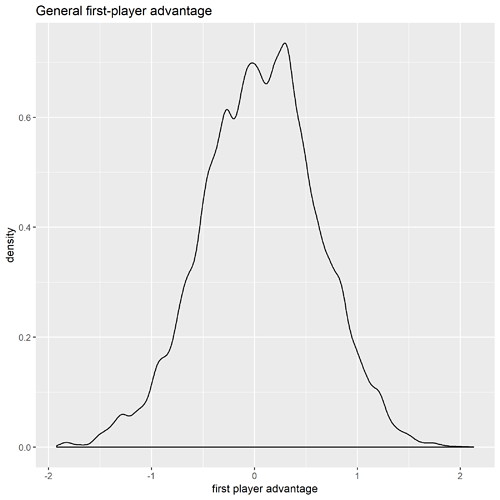
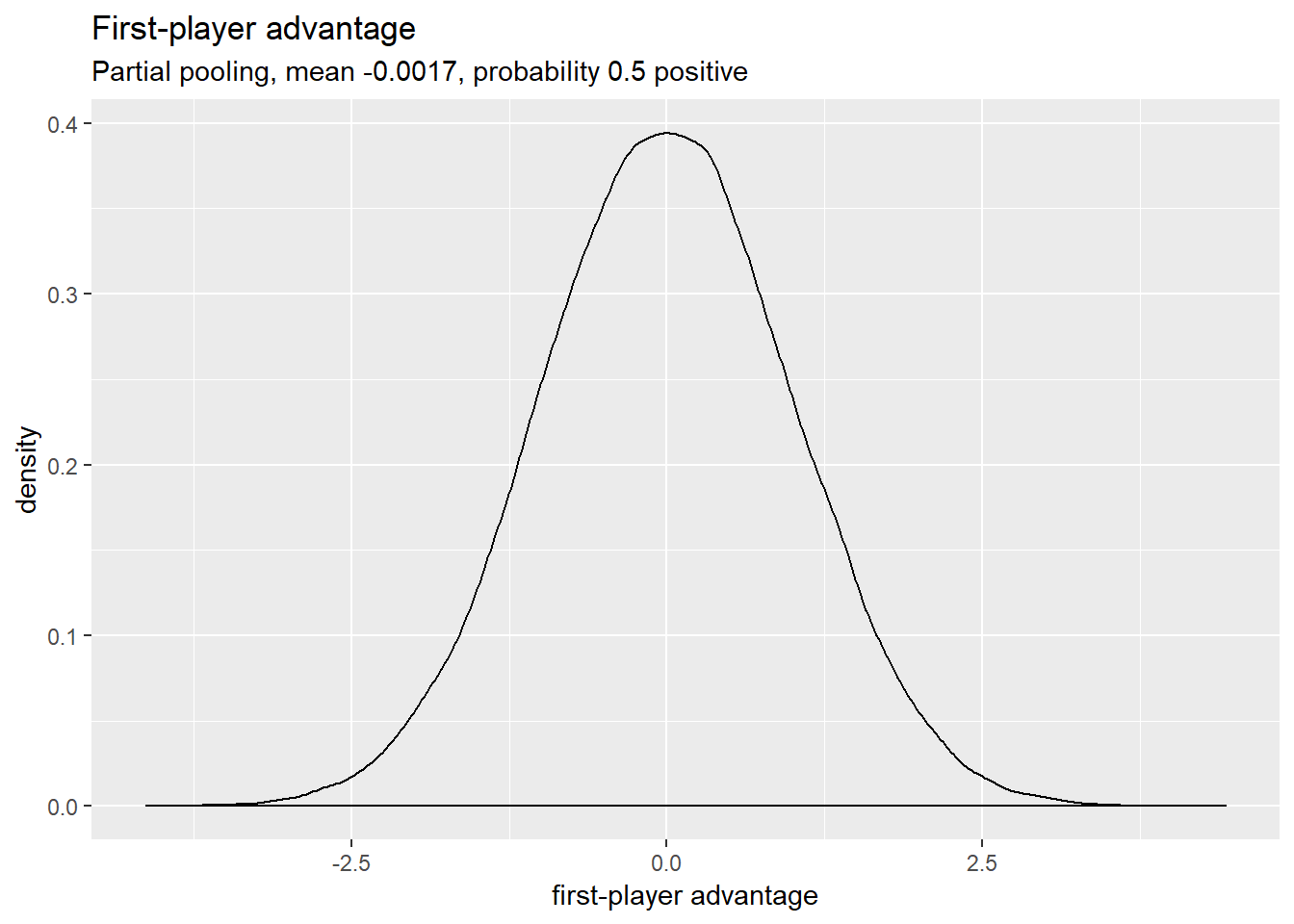
The model should make reasonably sane predictions before the data added, so we’re not waiting for 20 years for enough data for the model to make useful conclusions. Here’s what the distributions for first-turn advantage looks like:
Prior first-player advantage
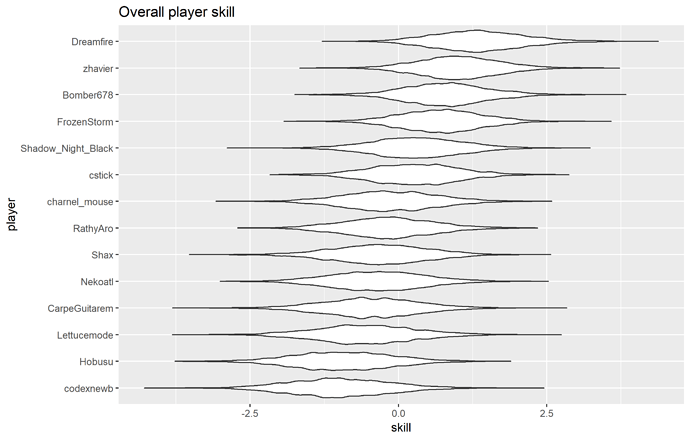
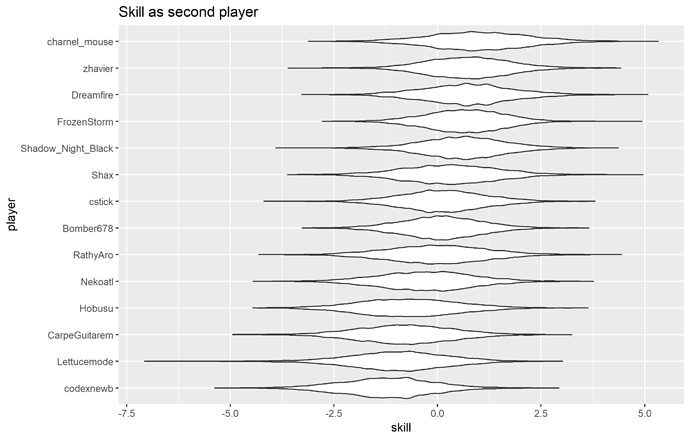
And here’s what the player skill distributions look like (players are interchangeable here):
Main player effect distributions
Prior distributions for starter and deck strengths are the same as for player skills.
For reference, first-player advantage, player skill, and deck strength are adjustments to the log-odds of winning. Log-odds look roughly like this:
| Victory log-odds |
Victory probability |
| -2.20 |
0.1 |
| -1.39 |
0.2 |
| -0.85 |
0.3 |
| -0.41 |
0.4 |
| 0.00 |
0.5 |
| 0.41 |
0.6 |
| 0.85 |
0.7 |
| 1.39 |
0.8 |
| 2.20 |
0.9 |
Player skills, and the rest, are mostly in the log-odds range from -2 to 2. That’s pretty swingy, but not completely implausible, so these priors aren’t too bad. I’d rather be under- than over-certain.
I don’t care. Show me the results.
OK, OK.
Turn order
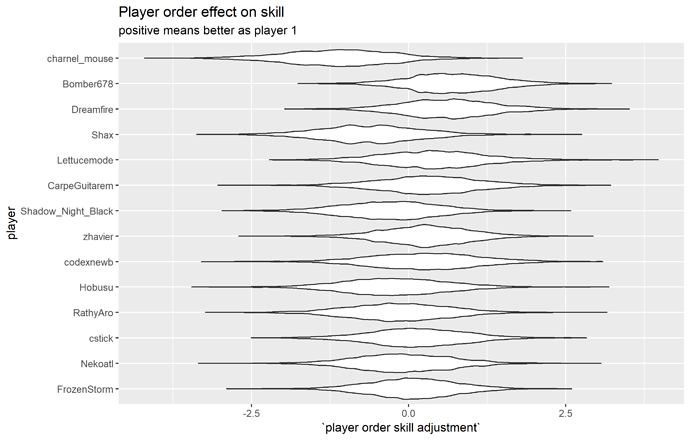
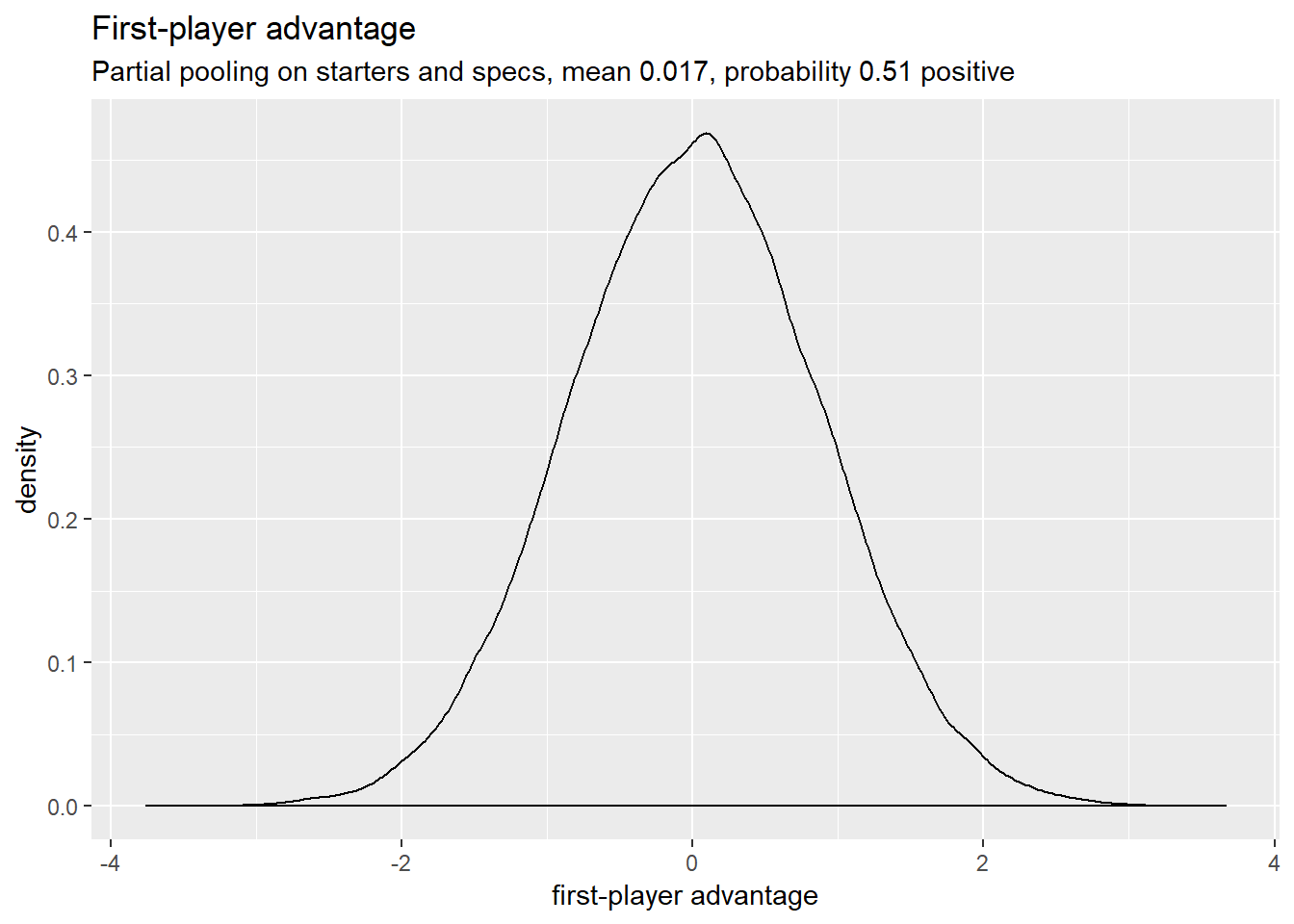
First-turn advantage
Player order makes no discernible difference. Maybe a slight advantage to player 1.
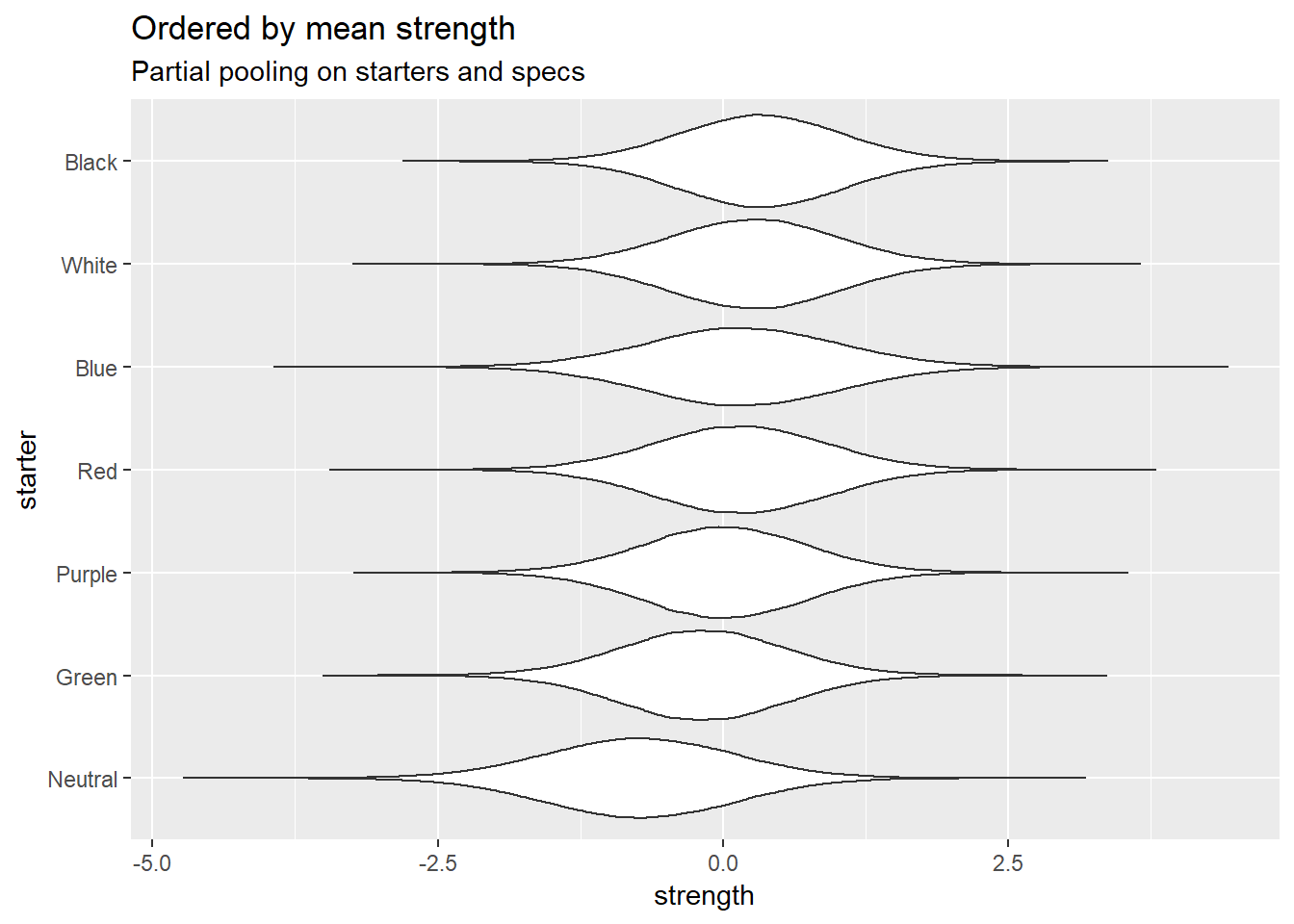
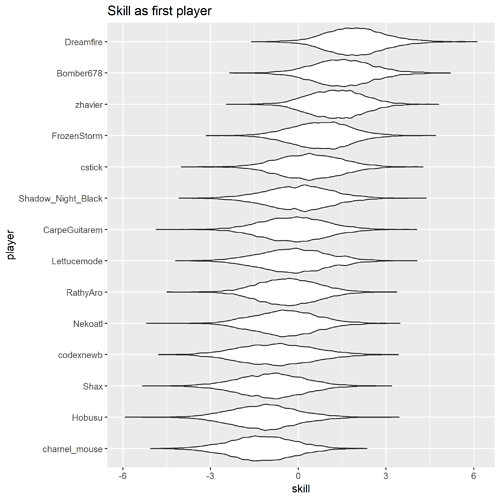
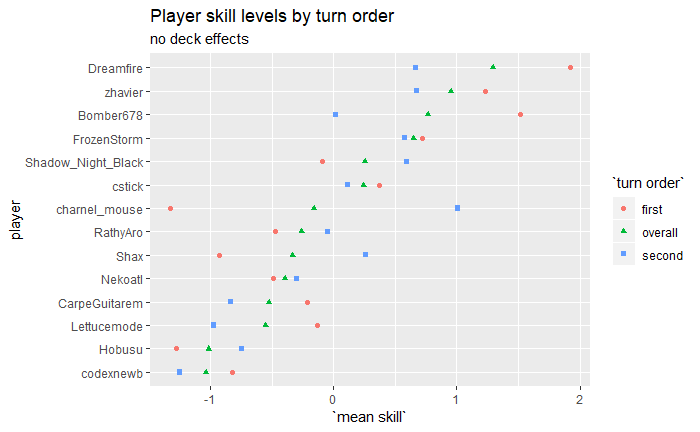
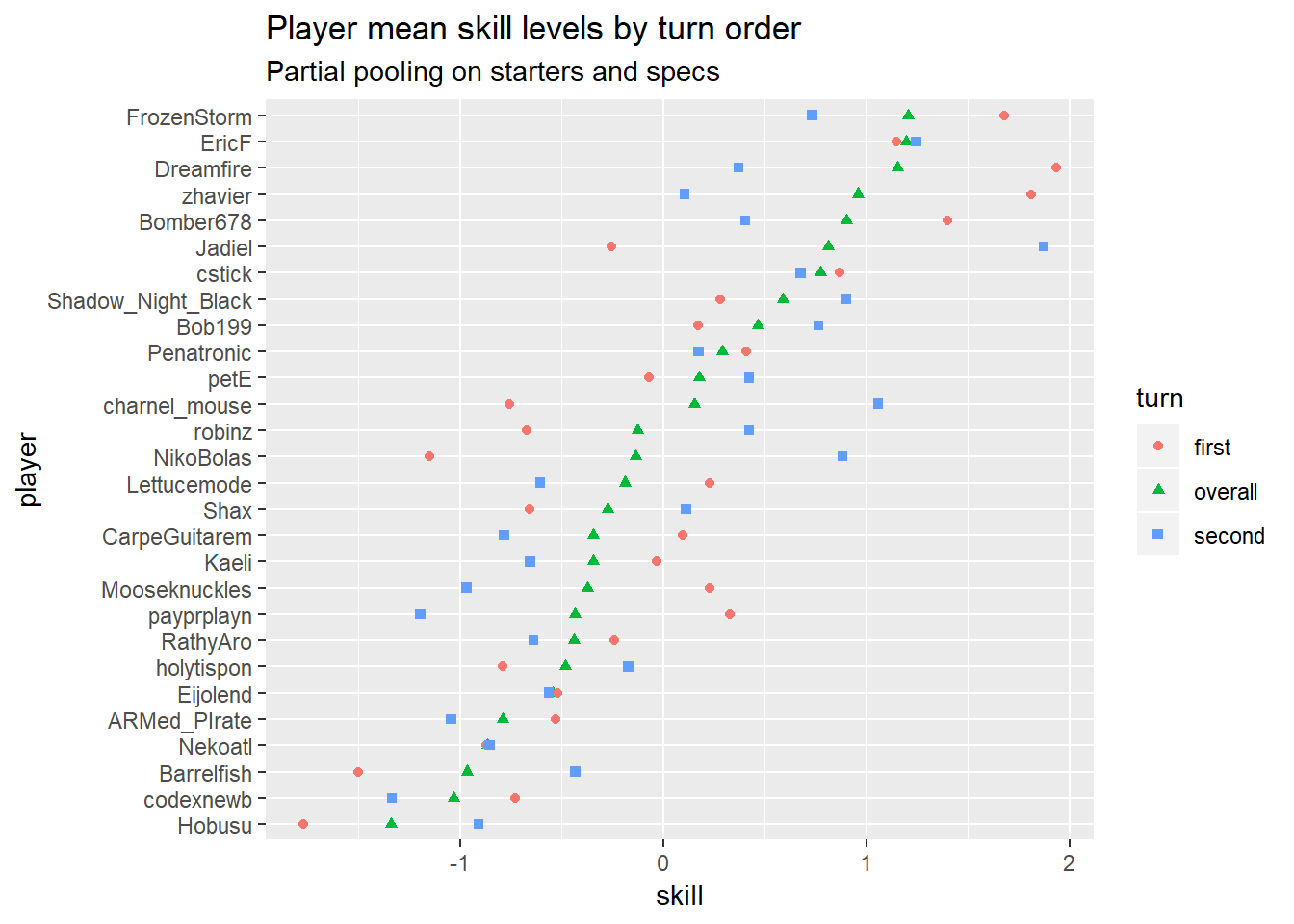
Player skill
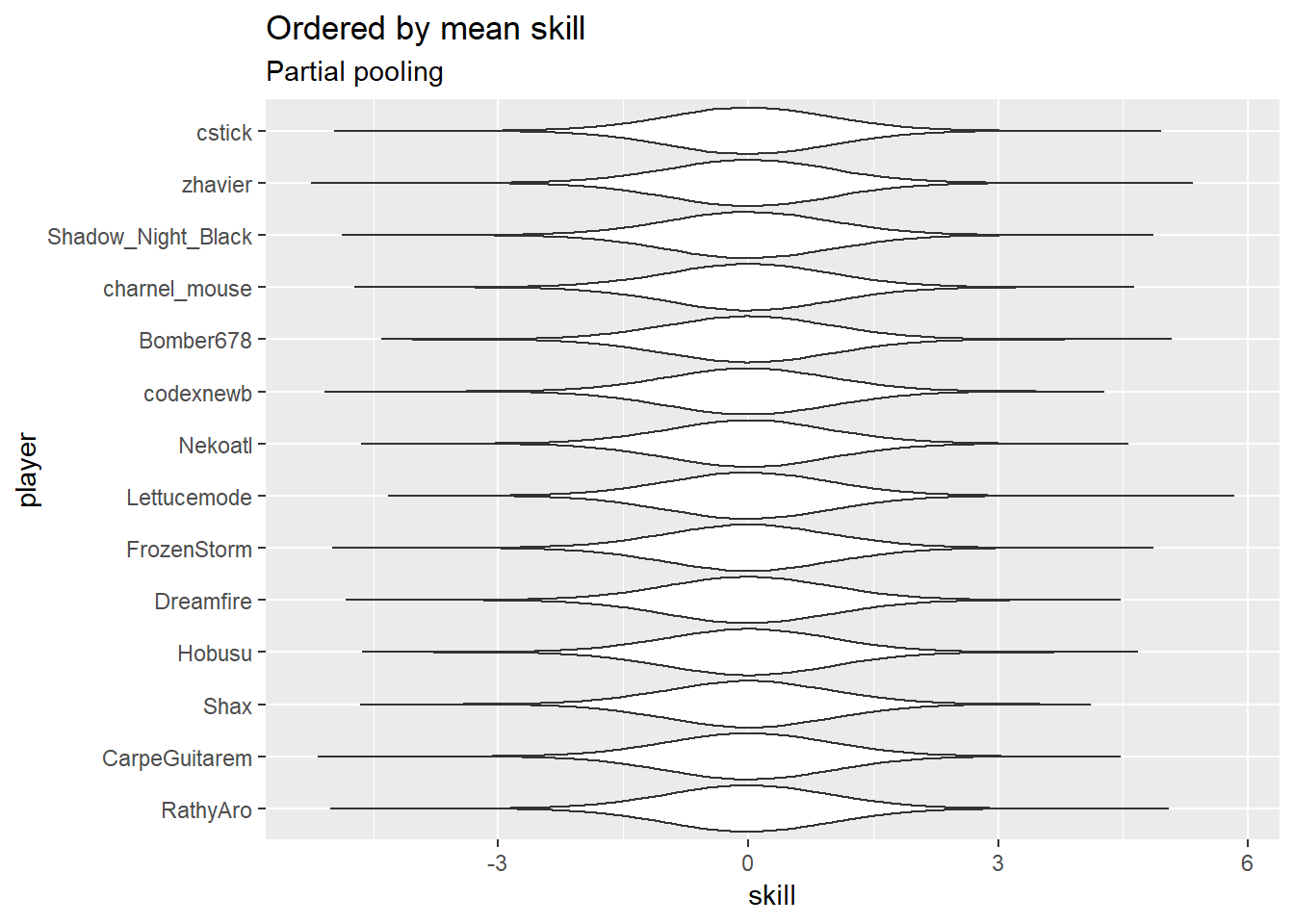
Average player skill levels
I have no idea what to make of the player skill predictions, given how many of these players vanished before I got here 
The top few players look about right, I’m not so sure about the rest. There are a few players who are automatically in the middle because they haven’t played enough in these tournaments for the model to get much information on their skill level (e.g. Kaeli, with a single non-timeout match), so that will throw the ordering off what might be expected.
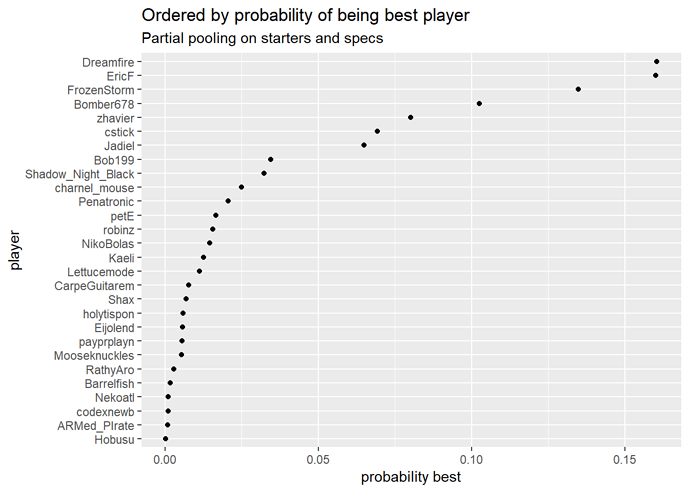
I also have plots giving the probability each player is the best. This is the one for overall skill, I have plots by turn order too if people want them. These plots take account of uncertainty where the average skill plots don’t, so these are probably more helpful.
Probability of each player being the best
The two highest-ranking players are only at about 16% each of being the best, so the rankings could still change dramatically with more data.
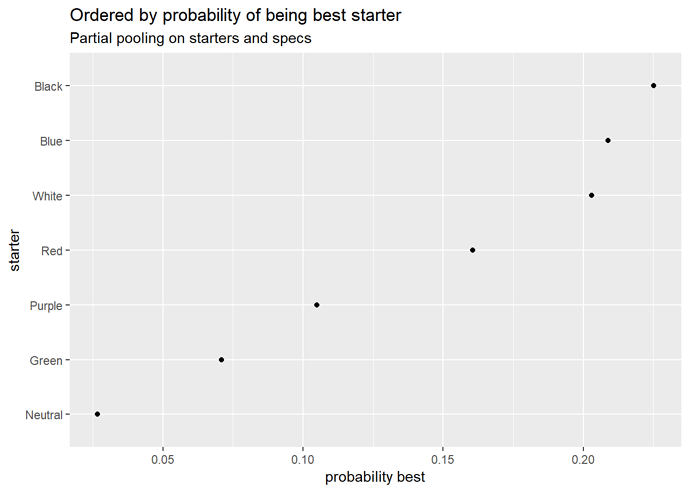
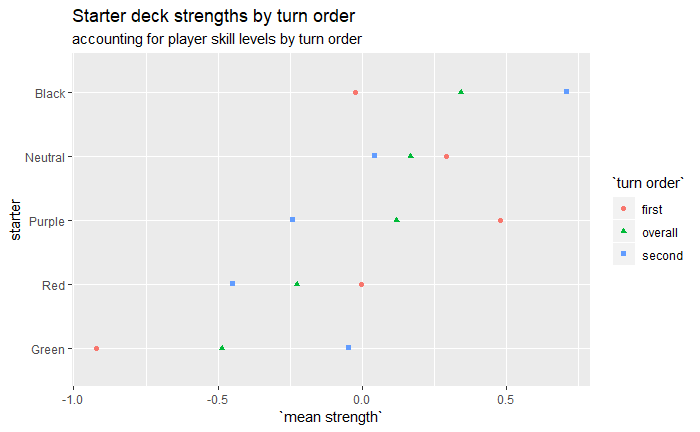
Deck strength
Here are the starter decks:
Overall starter strength
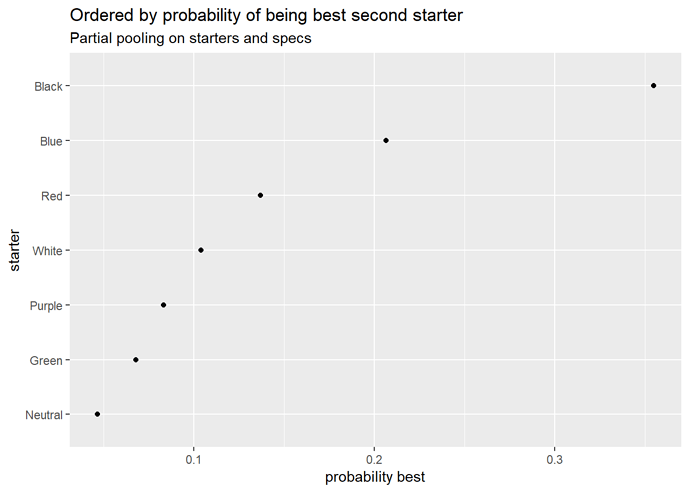
Neutral starter does really badly here.
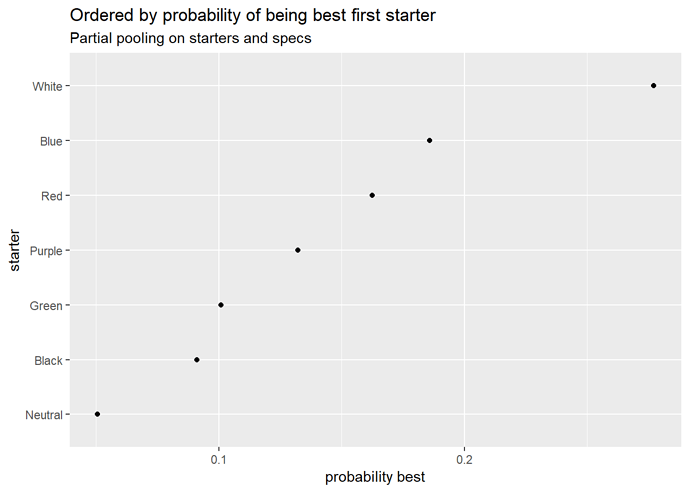
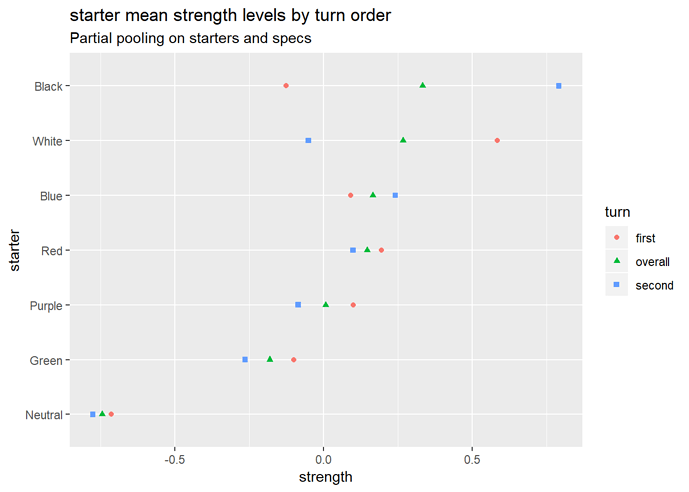
Starter strength by turn order
Yeah, I’m not too convinced by these at the moment. Bear in mind these are evaluations of the starters independent of the specs they’re paired with, but they still look pretty odd.
Summary plot for starter deck strengths
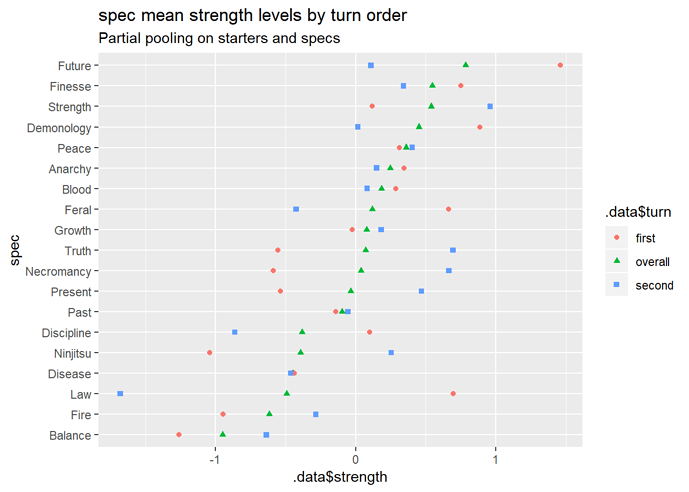
Now for the specs.
Summary plot for spec strengths
These look like a mess at the moment, too, so I’m going to skip over the other spec plots and move on to matchup predictions.
How much should we trust these results?
Well, you’ve probably looked at the starter and spec results and decided not very much. I’d like something to evaluate the model with in addition to the opinion of the players, even if that takes priority. Therefore, I’ve asked the model for post-hoc predictions for the outcome of all the matches. This is cheating a bit, because I’m using the data used to fit the model to evaluate, but it should give a rough idea of how it’s doing.
First of all, we can look at the matches where the model didn’t think a match would go the way it did. Here’s the top 10 “upsets” in the model’s opinion.
| Match |
Modelled probability of outcome |
| CAMS 2018 FrozenStorm Nightmare vs. zhavier Miracle Grow , won by zhavier |
0.29 |
| CAPS 2017 zhavier Miracle Grow vs. EricF Peace/Balance/Anarchy , won by EricF |
0.32 |
| CAPS 2017 FrozenStorm Nightmare vs. petE Miracle Grow , won by petE |
0.36 |
| CAMS 2018 cstick Finesse/Present/Discipline vs. RathyAro Nightmare , won by cstick |
0.39 |
| CAPS 2017 Penatronic Present/Peace/Blood vs. robinz Discipline/Fire/Truth , won by robinz |
0.40 |
| CAMS 2018 RathyAro Nightmare vs. Nekoatl Demonology/Strength/Growth , won by RathyAro |
0.44 |
| CAPS 2017 Jadiel Feral/Future/Truth vs. EricF Peace/Balance/Anarchy , won by Jadiel |
0.47 |
| CAMS 2018 zhavier Miracle Grow vs. Dreamfire Demonology/Strength/Growth , won by Dreamfire |
0.47 |
| CAMS 2018 zhavier Miracle Grow vs. FrozenStorm Nightmare , won by zhavier |
0.48 |
| CAMS 2017 Shadow_Night_Black Feral/Present/Truth vs. zhavier Discipline/Present/Anarchy , won by Shadow_Night_Black |
0.49 |
I haven’t had time to actually read through the matches, so if you have opinions about how unexpected these results are, let me know! What’s worth mentioning is that, out of the 108 matches I’ve current recorded, these are the only 10 matches where the model put the probability of the given outcome at less than 50%. A lot of the rest were thought to be pretty lopsided:
Distribution of post-hoc match predictions
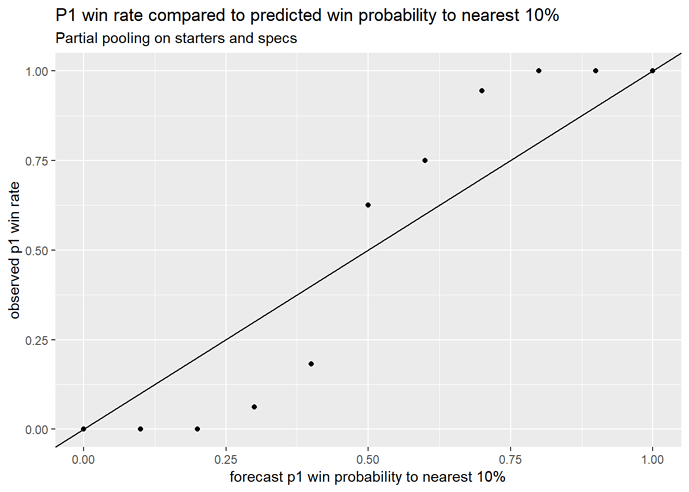
Now, we expect these to be thought of as lopsided to some extent: these are the matches used to fit the model, so it should be fairly confident about predicting them. So here’s a finer breakdown, where we roughly compare the model’s predicted outcome to how often it actually happened:
Predicted vs. actual player 1 win rate
It looks like the model’s predicted matchups aren’t lopsided enough! The matchups are even more extreme than it thinks they are.
What’s next?
This is where the model is at right now. It’s got some promise, I think, but it desperately needs, as a bare minimum, more data, and to take account of starter/spec synergies before its skill/strength results are really reliable.
Current plans
Next I’ll be allowing for starter/spec pairings to have an effect on deck strength, in addition to their individual effects. Hopefully we’ll see decks like Nightmare and Miracle Grow rapidly climb to the top of the charts.
I also need to add more match data. I don’t want to go too far back in time yet, because then the change in player skills over time will become something I need to worry about, so I’ll be adding results from the LDT series first.
Anything I can help with that doesn’t involve understanding the statistics spiel?
The most helpful thing I could get right now is anything odd on the current results set that I haven’t picked up on. I know the deck evaluations are a bit weird. Feedback on the current player ranking would be nice, if it won’t start fights. Most immediately helpful would be thoughts on the top 10 upsets list, as currently ranked by the model. Do these match results seem particularly surprising, in hindsight? Would you expect them to go the same way if they were played again?
Stop filling the forums up with so many images
If that’s a problem, I can just put the model up on GitHub, and occasionally bump the thread when I do a big update. Unless I get told otherwise, I’ll just post images for now.
Show me the stats!
Stan model code
data {
int<lower=0> M; // number of matches
int<lower=0> P; // number of players
int<lower=0> St; // number of starter decks
int<lower=0> Sp; // number of specs
int<lower=1> first_player[M]; // ID number of first player
int<lower=1> second_player[M]; // ID number of second player
int<lower=1> first_starter[M]; // ID number of first starter deck
int<lower=1> second_starter[M]; // ID number of second starter deck
int<lower=1> first_specs1[M]; // ID number for first player's first spec
int<lower=1> first_specs2[M]; // ID number for first player's second spec
int<lower=1> first_specs3[M]; // ID number for first player's third spec
int<lower=1> second_specs1[M]; // ID number for second player's first spec
int<lower=1> second_specs2[M]; // ID number for second player's second spec
int<lower=1> second_specs3[M]; // ID number for second player's third spec
int<lower=0, upper=1> w[M]; // 1 = first player wins, 0 = second player wins
}
parameters {
real turn; // first-player advantage in log odds
vector[P] player_std; // player skill levels in log odds effect
vector[P] player_turn_std; // player skill level adjustment for going first (penalty if second)
vector[St] starter_std; // starter deck strengths
vector[St] starter_turn_std; // starter deck strength adjustment for going first (penalty if second)
vector[Sp] spec_std; // spec strength
vector[Sp] spec_turn_std; // spec strength adjustment for going first
real lsd_player; // player skill log spread
real lsd_player_turn; // player skill turn adjustment log spread
real lsd_starter; // starter deck strength log spread
real lsd_starter_turn; // starter deck strength turn adjustment log spread
real lsd_spec; // spec strength log spread
real lsd_spec_turn; // spec strength log turn adjustment spread
}
transformed parameters{
vector[M] matchup; // log-odds of a first-player win for each match
real<lower=0> sd_player = exp(lsd_player);
real<lower=0> sd_player_turn = exp(lsd_player_turn);
real<lower=0> sd_starter = exp(lsd_starter);
real<lower=0> sd_starter_turn = exp(lsd_starter_turn);
real<lower=0> sd_spec = exp(lsd_spec);
real<lower=0> sd_spec_turn = exp(lsd_spec_turn);
vector[P] player = sd_player * player_std;
vector[P] player_turn = sd_player_turn * player_turn_std;
vector[St] starter = sd_starter * starter_std;
vector[St] starter_turn = sd_starter_turn * starter_turn_std;
vector[Sp] spec = sd_spec * spec_std;
vector[Sp] spec_turn = sd_spec_turn * spec_turn_std;
matchup = turn +
player[first_player] + player_turn[first_player] - player[second_player] + player_turn[second_player] +
starter[first_starter] - starter[second_starter] + starter_turn[first_starter] + starter_turn[second_starter] +
spec[first_specs1] - spec[second_specs1] + spec_turn[first_specs1] + spec_turn[second_specs1] +
spec[first_specs2] - spec[second_specs2] + spec_turn[first_specs2] + spec_turn[second_specs2] +
spec[first_specs3] - spec[second_specs3] + spec_turn[first_specs3] + spec_turn[second_specs3];
}
model {
lsd_player ~ normal(0, 0.1);
lsd_player_turn ~ normal(0, 0.1);
lsd_starter ~ normal(0, 0.1);
lsd_starter_turn ~ normal(0, 0.1);
lsd_spec ~ normal(0, 0.1);
lsd_spec_turn ~ normal(0, 0.1);
turn ~ std_normal();
player_std ~ std_normal();
player_turn_std ~ std_normal();
starter_std ~ std_normal();
starter_turn_std ~ std_normal();
spec_std ~ std_normal();
spec_turn_std ~ std_normal();
w ~ bernoulli_logit(matchup);
}
What's this "partial pooling" you're referring to in the plot subtitles?
Partial pooling is a statistical technique often used by Stan users, and people who read the work of Andrew Gelman, and is a type of hierarchical model.
As an example, I previously had all the player skill levels modelled as independent. That gives reasonable results, but partial pooling lets me control how large the levels can get, and also introduces some dependency.
Specifically, whereas before each skill level had an independent Normal(0, 1) distribution, they now all have an independent Normal(0, sd) distribution, where sd is an additional unknown parameter for the model to do inference on (these are the lsd_... and sd_... variables in the Stan model code above). So, if a player’s skill is considered to be large, then sd will be pushed to be larger, and the other player skill will tend to spread out a bit more too. Statistically, this has a “shrinkage” effect, that stops any of the estimated skill/strength levels from becoming infeasible large at the expense of everything else.
This is useful for two other reasons. Firstly, the use of an sd variable means that first-player advantage, player skill, starter strength etc. can now have a different average size of effect. If the sd for player skill tends to be larger, that means player skill is considered to tend to have a larger effect on matchup compared to first-turn advantage. Secondly, sd for e.g. player skill determines the general population that the modelled players’ skill levels are drawn from. This means that inference on sd translates to inference on what we expect the skill level of non-modelled players to look like. Has a new player just appeared? sd will help give an a priori idea of what their skill level might look like.
It’s called partial pooling in comparison to, e.g., modelling all player skill levels as exactly the same (complete pooling), or treating them all independently (no pooling).
The top few players look about right, I’m not so sure about the rest. There are a few players who are automatically in the middle because they haven’t played enough in these tournaments for the model to get much information on their skill level (e.g. Kaeli, with a single non-timeout match), so that will throw the ordering off what might be expected.
