Yeah, that would really helpful, thank you!
I’ve tried some more complex version of the model, but it didn’t seem to make much difference to the results – if anything, it made the predictive performance worse. At this point, the thing I need most is more data. I’ll keep plugging away at adding results from the Seasonal Swiss tournaments.
I’ve also rejigged the format of the main data file, so that it’s hopefully easier to add match data:
- Deck information for each player is now done per match.
- Instead of giving deck information in 4 columns (starter, 3 specs), there’s now a single column for the deck’s name in forum format, e.g. [Balance]/Blood/Strength. I’ll go through and standardise the deck names. Just make sure the slashes are there, and the first spec is one for the starter deck. For example, Balance/Strength/Growth with the Green starter is fine, Strength/Balance/Growth with the Green starter is not. You don’t need the brackets. Alternatively, you can add a deck’s nickname to the nickname sheet, and enter that instead. I’ve already added some common ones: MonoRed etc., Nightmare, Miracle Grow, and some others.
- There’s also a new column for match format (forum/Tabletopia/face-to-face), so I can start using the data kindly collected by Metalize.
- There’s an optional column to indicate that the player order in a match is unknown. If it’s known, just leave it blank.
If there’s anything else that you think would make entry easier, please let me know.
Current to-do list includes adding more match data, and maybe putting my modelling work up on GitHub so people can laugh at my terrible Stan code see the details if they’re curious.
Another quick update. I’m still working on this, slowly.
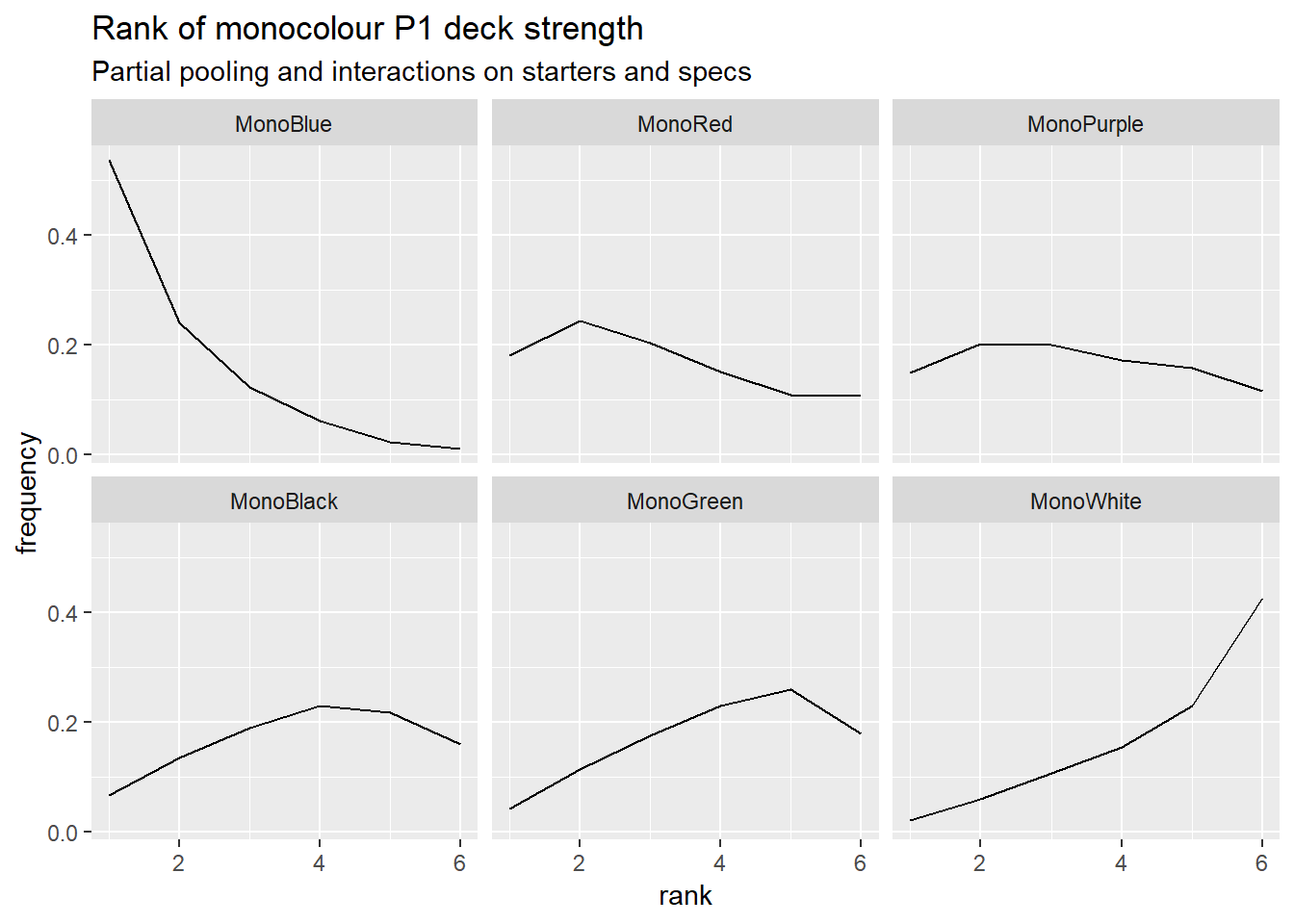
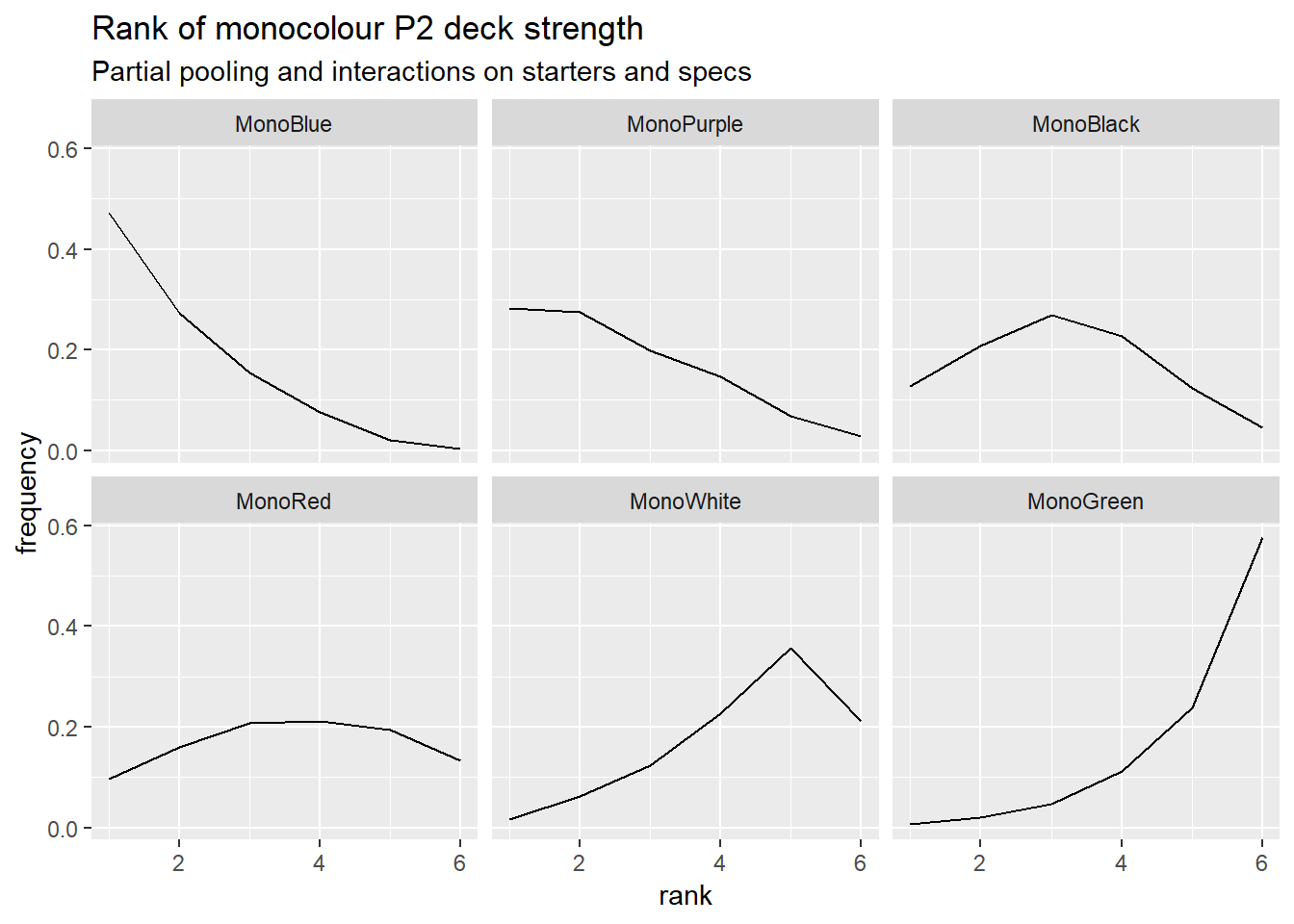
I’ve now added interactions between starter decks and specs, and between specs, to account for synergies. It’s improved the model’s post-hoc predictions on match results a little. I don’t think it’s currently worth a full post yet, because it still has a problem the previous versions had that I didn’t mention before. Here are the model’s rankings for the monocolour decks, low rank is better. See if you can spot the problem.
I think I need to let a deck’s strength be dependent on which deck it’s facing. Full-length post next time if that sorts things out.
OK, I fixed the problem, but it was nothing to do with the model. It was because I’d misrecorded the Black vs. Blue MMM1 matches as all being won by Blue. Ho, ho, ho. I know what I’m doing.
I’ve changed the model anyway, so here’s another update. Not as thorough as last time, my brain’s a bit burnt-out at the moment.
Data status
I’ve added match results for CAWS18 and XCAPS19. I’m leaving CAMS19 results until the tournament finishes. In the meantime, I’ll get the model to predict CAMS19 match results from previous data to see how well it does, and post about it after the tournament’s over.
Model structure
Previously, each deck (or starter, or spec) was assigned a single strength value, so the decks were effectively ranked on a one-dimensional scale. In hindsight, this wasn’t very likely to work well: the strength of a deck is going to depend on the opposing deck.
For example, Nightmare ([Demonology/Necromancy]/Finesse) is a very strong deck, but isn’t so great against Miracle Grow ([Anarchy]/Growth/Strength). Similarly, the usefulness of a particular spec in your deck depends on what you’re facing. Going for a Growth deck for Might of Leaf and Claw? Probably not so great against specs with upgrade removal and/or ways to easily deal with Blooming Ancients. Some specs are a lot stronger than others, but they aren’t no-brainers that are great against everything. Well, most of them aren’t. ![]()
I’ve therefore complected the model to only work in terms of opposing pairs. Starter vs. starter, starter vs. spec, spec vs. spec. As before, these each have an additive effect on the log-odds of a player-one victory.
Player skills are still treated individually, not in opposed pairs: I think ranking players on a simple scale makes sense. Also, the main goal here is to evaluate deck strengths, so I’d like to keep player effects simple so I can worry about more important things.
New results
Turn order
I’m no longer tracking first-player advantage. It’s now effectively part of the deck strengths, because, e.g., Red vs. Green is tracked separately from Green vs. Red (P1 component first).
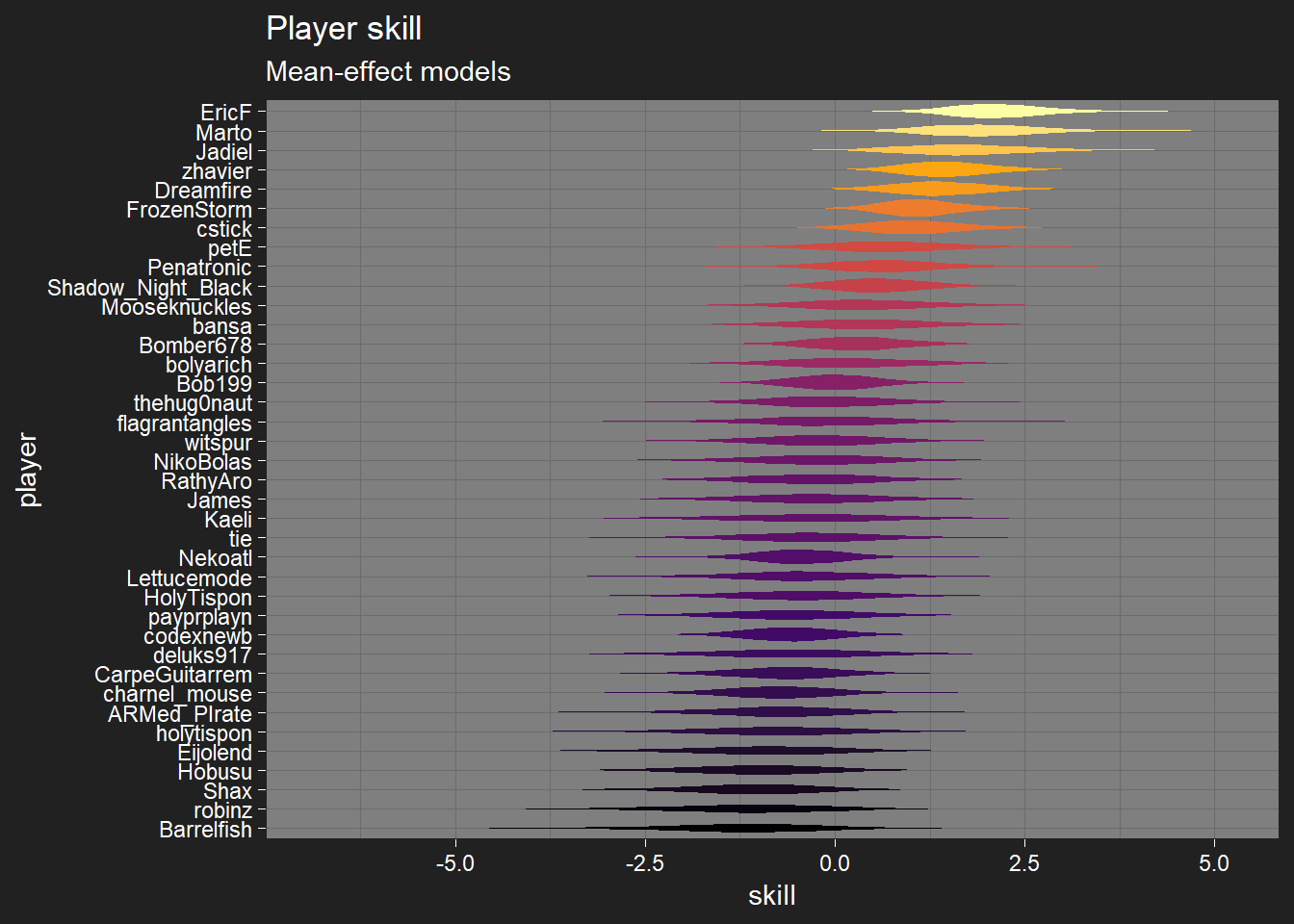
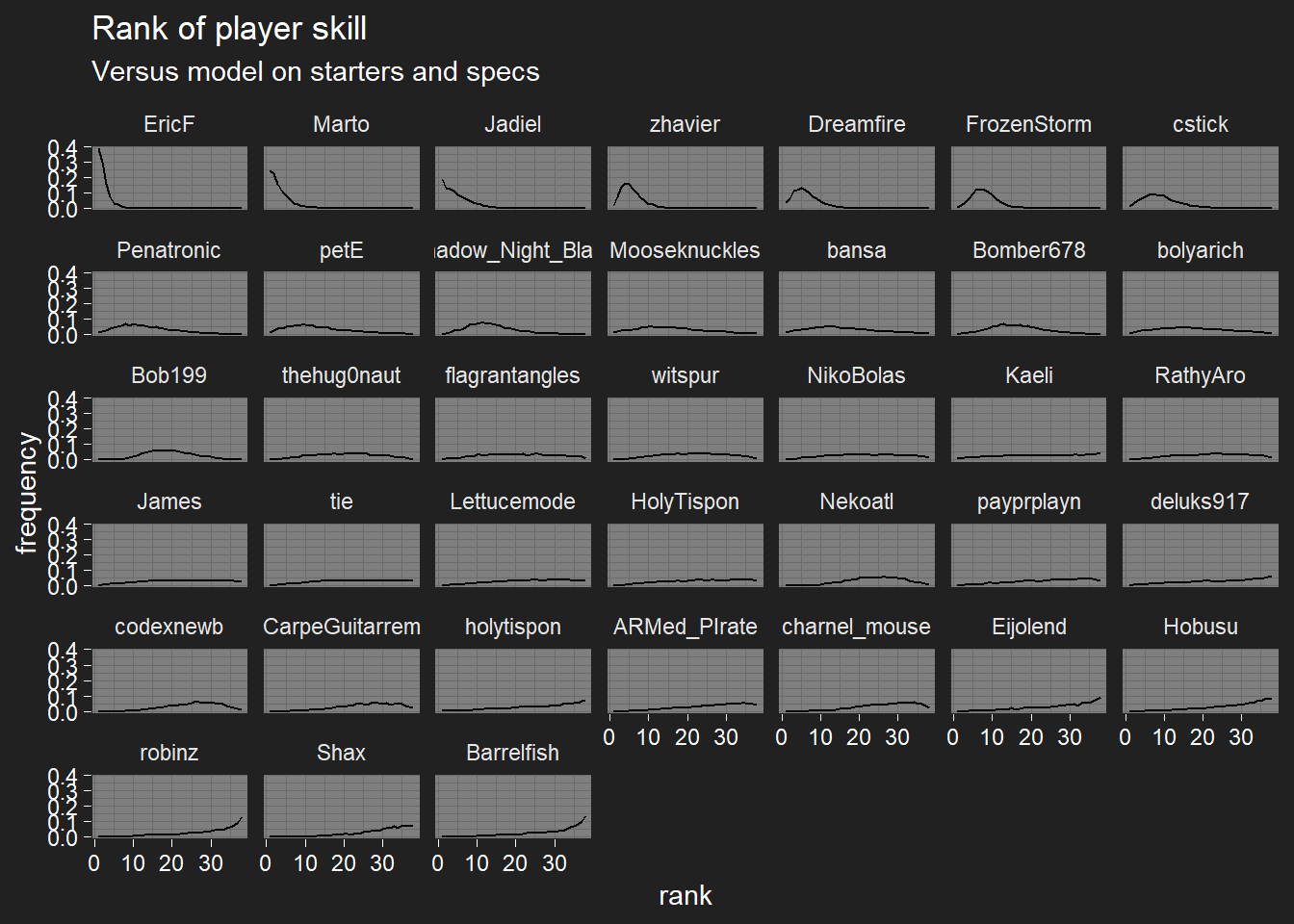
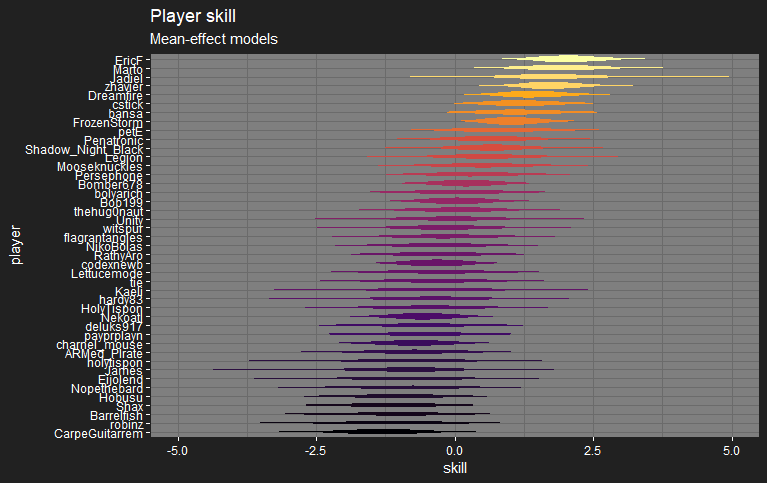
Player skill
I’ve removed turn-order effects from player skill for the moment, so I can focus more on deck effects. Skills are on the log-odds-effect scale.
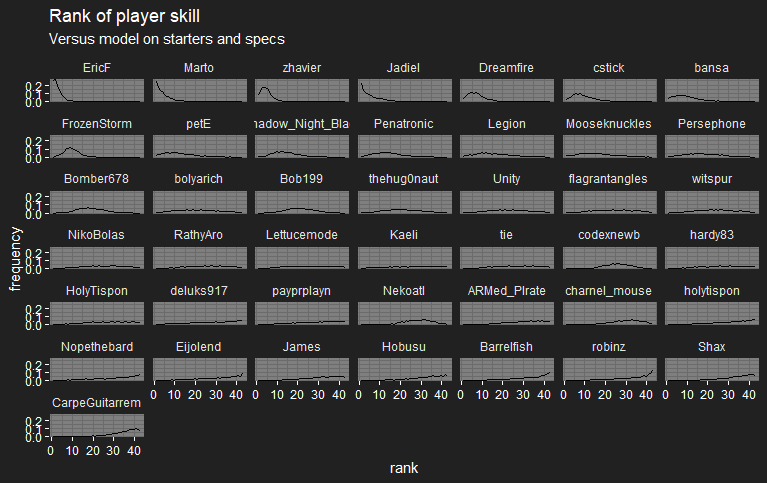
I’ve also switched to plotting each player’s rank distribution instead of just their probability of being the best player, hopefully it’s a bit more informative.
Deck strengths
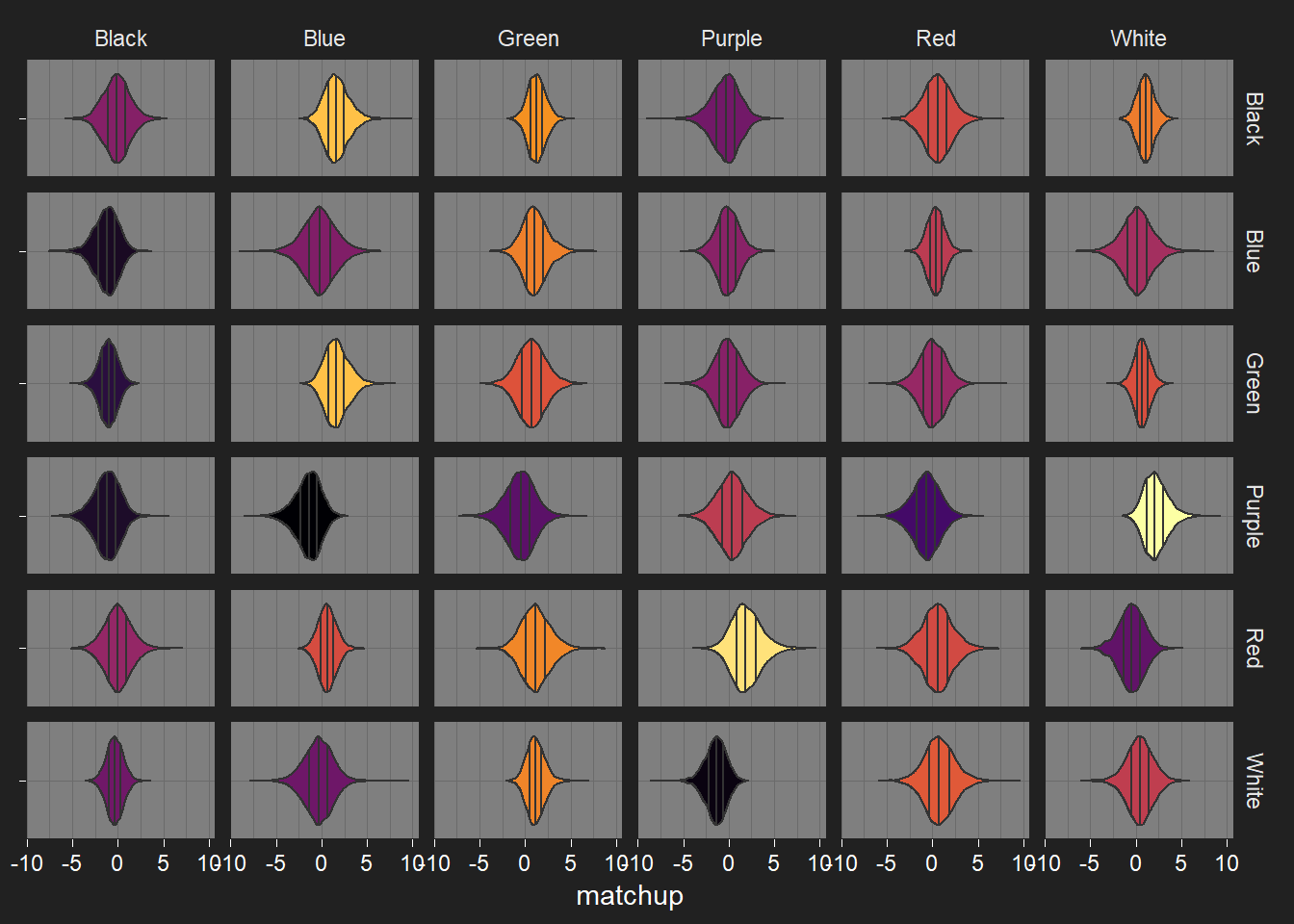
Because of the switch to looking at opposed pairs, plots showing the strengths for all the different components are now incredibly ungainly. Because of this, I’m just posting the predicted matchups between the monocolour decks, and can put up matchups for other decks later (the ones with a nickname, perhaps). Player 1 on the rows, Player 2 on the columns.
Numeric summaries for the matchups below. I’ll put up a similar table for the recorded matches used to fit the model, when I’ve got the time.
Numerical monocolour matchup details
I’m not entirely sure how useful this table is going to be in a Discourse post: in my IDE this is a DataTable, so I can easily sort by different columns. I’ve sorted them by matchup fairness here.
P1/P2 deck are the monocolour decks used. Matchup is the average P1 win probability, written in the x–(10-x) matchup notation that’s used in Yomi. Fairness depends on how far the average P1 win probability is from the perfectly-balanced 50% win probability: a 5-5 matchup has fairness 1, 0-10 and 10-0 matchups have fairness 0.
| Match ID | P1 deck | P2 deck | P1 win probability | matchup | fairness |
|---|---|---|---|---|---|
| 25 | Red | Black | 0.498 | 5.0-5.0 | 1.00 |
| 17 | Green | Red | 0.506 | 5.1-4.9 | 0.99 |
| 10 | Blue | Purple | 0.479 | 4.8-5.2 | 0.96 |
| 16 | Green | Purple | 0.479 | 4.8-5.2 | 0.96 |
| 1 | Black | Black | 0.474 | 4.7-5.3 | 0.95 |
| 12 | Blue | White | 0.524 | 5.2-4.8 | 0.95 |
| 8 | Blue | Blue | 0.467 | 4.7-5.3 | 0.93 |
| 4 | Black | Purple | 0.447 | 4.5-5.5 | 0.89 |
| 32 | White | Blue | 0.441 | 4.4-5.6 | 0.88 |
| 22 | Purple | Purple | 0.563 | 5.6-4.4 | 0.87 |
| 31 | White | Black | 0.428 | 4.3-5.7 | 0.86 |
| 11 | Blue | Red | 0.577 | 5.8-4.2 | 0.85 |
| 36 | White | White | 0.576 | 5.8-4.2 | 0.85 |
| 30 | Red | White | 0.416 | 4.2-5.8 | 0.83 |
| 21 | Purple | Green | 0.412 | 4.1-5.9 | 0.82 |
| 5 | Black | Red | 0.600 | 6.0-4.0 | 0.80 |
| 29 | Red | Red | 0.598 | 6.0-4.0 | 0.80 |
| 15 | Green | Green | 0.622 | 6.2-3.8 | 0.76 |
| 23 | Purple | Red | 0.379 | 3.8-6.2 | 0.76 |
| 26 | Red | Blue | 0.629 | 6.3-3.7 | 0.74 |
| 35 | White | Red | 0.628 | 6.3-3.7 | 0.74 |
| 18 | Green | White | 0.641 | 6.4-3.6 | 0.72 |
| 9 | Blue | Green | 0.692 | 6.9-3.1 | 0.62 |
| 27 | Red | Green | 0.691 | 6.9-3.1 | 0.62 |
| 13 | Green | Black | 0.296 | 3.0-7.0 | 0.59 |
| 19 | Purple | Black | 0.295 | 3.0-7.0 | 0.59 |
| 6 | Black | White | 0.713 | 7.1-2.9 | 0.57 |
| 7 | Blue | Black | 0.282 | 2.8-7.2 | 0.56 |
| 33 | White | Green | 0.723 | 7.2-2.8 | 0.55 |
| 3 | Black | Green | 0.744 | 7.4-2.6 | 0.51 |
| 20 | Purple | Blue | 0.256 | 2.6-7.4 | 0.51 |
| 34 | White | Purple | 0.245 | 2.5-7.5 | 0.49 |
| 2 | Black | Blue | 0.780 | 7.8-2.2 | 0.44 |
| 14 | Green | Blue | 0.782 | 7.8-2.2 | 0.44 |
| 28 | Red | Purple | 0.796 | 8.0-2.0 | 0.41 |
| 24 | Purple | White | 0.846 | 8.5-1.5 | 0.31 |
Model code
Comments might be out of date, take with a pinch of salt.
Stan code
data {
int<lower=0> M; // number of matches
int<lower=0> P; // number of players
int<lower=0> St; // number of starter decks
int<lower=0> Sp; // number of specs
int<lower=1> first_player[M]; // ID number of first player
int<lower=1> second_player[M]; // ID number of second player
int<lower=1> first_starter[M]; // ID number of first starter deck
int<lower=1> second_starter[M]; // ID number of second starter deck
int<lower=1> first_specs1[M];
int<lower=1> first_specs2[M];
int<lower=1> first_specs3[M];
int<lower=1> second_specs1[M];
int<lower=1> second_specs2[M];
int<lower=1> second_specs3[M];
int<lower=0, upper=1> w[M]; // 1 = first player wins, 0 = second player wins
}
parameters {
vector[P] player_std; // player skill levels in log odds effect
matrix[St, St] starter_vs_starter_std; // starter vs. starter effect in log odds
matrix[St, Sp] starter_vs_spec_std; // starter vs. spec effect in log odds
matrix[Sp, St] spec_vs_starter_std; // spec vs. starter effect in log odds
matrix[Sp, Sp] spec_vs_spec_std; // spec vs. spec effect in log odds
real<lower=0> sd_player; // player skill spread
real<lower=0> sd_starter_vs_starter; // starter vs. starter effect spread
real<lower=0> sd_starter_vs_spec; // starter vs. spec effect (or vice versa) spread
real<lower=0> sd_spec_vs_spec; // spec vs. spec effect spread
}
transformed parameters {
vector[M] matchup; // log-odds of a first-player win for each match
vector[P] player = sd_player * player_std;
matrix[St, St] starter_vs_starter = sd_starter_vs_starter * starter_vs_starter_std;
matrix[St, Sp] starter_vs_spec = sd_starter_vs_spec * starter_vs_spec_std;
matrix[Sp, St] spec_vs_starter = sd_starter_vs_spec * spec_vs_starter_std;
matrix[Sp, Sp] spec_vs_spec = sd_spec_vs_spec * spec_vs_spec_std;
for (i in 1:M) {
matchup[i] = player[first_player[i]] - player[second_player[i]] +
starter_vs_starter[first_starter[i], second_starter[i]] +
starter_vs_spec[first_starter[i], second_specs1[i]] +
starter_vs_spec[first_starter[i], second_specs2[i]] +
starter_vs_spec[first_starter[i], second_specs3[i]] +
spec_vs_starter[first_specs1[i], second_starter[i]] +
spec_vs_starter[first_specs2[i], second_starter[i]] +
spec_vs_starter[first_specs3[i], second_starter[i]] +
spec_vs_spec[first_specs1[i], second_specs1[i]] +
spec_vs_spec[first_specs1[i], second_specs2[i]] +
spec_vs_spec[first_specs1[i], second_specs3[i]] +
spec_vs_spec[first_specs2[i], second_specs1[i]] +
spec_vs_spec[first_specs2[i], second_specs2[i]] +
spec_vs_spec[first_specs2[i], second_specs3[i]] +
spec_vs_spec[first_specs3[i], second_specs1[i]] +
spec_vs_spec[first_specs3[i], second_specs2[i]] +
spec_vs_spec[first_specs3[i], second_specs3[i]];
}
}
model {
sd_player ~ lognormal(0, 0.5);
sd_starter_vs_starter ~ lognormal(0, 0.5);
sd_starter_vs_spec ~ lognormal(0, 0.5);
sd_spec_vs_spec ~ lognormal(0, 0.5);
player_std ~ std_normal();
for (i in 1:St) {
starter_vs_starter_std[i, ] ~ std_normal();
starter_vs_spec_std[i, ] ~ std_normal();
}
for (i in 1:Sp) {
spec_vs_starter_std[i, ] ~ std_normal();
spec_vs_spec_std[i, ] ~ std_normal();
}
w ~ bernoulli_logit(matchup);
}
Where to go from here?
Main items on the current to-do list:
- Put some more thought into the prior distributions for the variance parameters. The new model structure makes more intuitive sense, I think, but I need to check it has the same prior as the other models, so I can check it’s better at matchup prediction.
- More data. CAMS19 when it finishes, but first I’m planning to integrate the data that @Metalize kindly put together (sorry for the delay!). I’m delaying adding data from older tournaments (i.e. the old forum), because I currently don’t account for player skills changing over time. This does shaft currently forum-inactive players like Hobusu, unfortunately.
- Evaluate the average influence of player skill vs. deck strength on the matchup. In theory, I can already do this, but my current plots aren’t as clear as I’d like them to be, so I need to tidy them up a bit before I put them up.
- Interaction terms between the opposed pairs. The thought of coding this fills me with dread, honestly, but without them the model currently doesn’t take account of inter-spec synergies at all.
- At some point I tried a different model, where the player skills were between 0 and 1, and were a multiplicative effect on the deck strength. This failed, but it might have been because of the Black vs. Blue issue I’ve now fixed. I think this is worth doing eventually, for the same reasons I suggested it for the Yomi model: it means that the model gives deck strengths under optimal play, instead of deck strengths under average play, and the former is what we’re more interested in.
- Tier lists! The end goal, really. This is a bit harder now decks aren’t rated on a single scale, but I can plug all the available decks into a zero-sum game, see how frequently they’re picked at the Nash equilibrium, and use that as their rating. I want to do more checks on the model’s predictive performance before I do this.
- There’s some other “cool” things I’d like to try once the model’s doing well. For example, I could pull up the predicted matchups in the Seasonal Swiss tournaments, and see whether the matches tend to become fairer in later rounds. My model’s also similar enough in structure to professional systems (Élő, Glicko, Trueskill) that I could try taking my model’s conclusions and showing how they’d work out under those other systems. For example, the variance parameters are analogies to TrueSkill’s beta parameter, that describes the height of a game’s skill ceiling (the Factor #2 section here).
- Anything else? Anything stand out as unusual in the monocolour matchups? (Purple vs. White stands out to me). Other matchup predictions you’d like to see? Does my Stan code suck? Yes, it does.
in the 0-10 images, what do the colors mean?
The colour is linked to the mean matchup value, and uses the viridis inferno palette. Lighter colours indicate a high mean P1 advantage, darker colours indicate a high mean P2 advantage.
This is very interesting. Thanks for poking at this!
I found the monocolour Nash equilibrium for the mean matchup values, rounded to two decimal places. To estimate optimal deck-picking strategy properly, I’d have to write code to calculate the equilibrium for each of the 4,000 samples to show the distribution for the Nash equilibrium, and we’d see more colour variety. But hey, I thought I’d do this simple version by hand, just for fun.
P1 strategy: Black 1 : Red 3. (i.e. randomly pick Black or Red, picking Black 1/4 of the time. Ignore other colours.)
P2 strategy: Black 29 : White 3.
Matchup: 4.925-5.075, very slightly P2-favoured.
Mixed strategy performance against pure strategies (i.e. pick the same deck every time):
| Black | Blue | Green | Purple | Red | White | |
|---|---|---|---|---|---|---|
| P1 versus… | 4.925 | 6.675 | 7.025 | 7.125 | 6.000 | 4.925 |
| P2 versus… | 5.075 | 6.975 | 6.681 | 6.484 | 5.075 | 5.559 |
This means that if the current model was to be trusted, Purple would be deemed off-meta. ![]()
EDIT
I didn’t describe very well what this actually means. If you’re playing a mono-colour match against someone as skilled as you, and you know who’s going first, and you trust the model’s current results (which is a big if), the above strategies would be what you’d do to maximise your chances of winning the match.
Matchups for the used decks work out like this:
| P1\P2 | Black | White |
|---|---|---|
| Black | 4.7 | 7.1 |
| Red | 5.0 | 4.2 |
Usually it’s an even Red/Black match, or Black/Black with a small advantage for P2. P2 sometimes goes for White for a small advantage against Red, but if P1 takes Black and catches him doing this, he gets punished really hard, so he does this very sparingly.
The “proper” method I mention above drives a different approach to choosing your deck:
- Draw a set of model parameters from the samples;
- For that set, find the Nash equilibrium;
- Use the resulting strategy to pick your deck.
This balances trying to win the match against getting more information about what the best strategy might be, and is known as Thompson sampling.
Slicing the data 36 ways, how many matches of data does each matchup have?
It would surprise me if there really were so many matchups in the 70-30 & worse range, given the design goals & how long Codex was in dev.
There are 317 recorded matches, but 14 ended in a timeout and I don’t use them. Additionally, 118 of the remaining matches have Bashing or Finesse present. Roughly, that leaves 250 matches’ worth of data that is relevant to the mono-colour matches, about 7 matches per matchup. They’re nowhere near evenly distribution though: Black specs are more popular, for example, and some MMM1 matchups were never played.
As far as the number of lopsided matches goes, there are two things happening:
- Amount of data. Obviously, this will improve. Not just number of matches, but as I add more tournaments and players vary their decks, player skills will be better disentangled from deck strengths (not perfectly, good players also tend to pick good decks). It’ll be a slow improvement for the mono-colour case, because almost no one uses mono-colour decks in tournaments. Time for an MMM revival? There are also some recent-ish tournaments I haven’t added yet, i.e. RACE.
- I haven’t yet put enough thought into the prior beliefs for the possible spread of player skills and deck strengths. I want to set them up along the lines of “all/most of the matchups between evenly-skilled players should fall in this range”, and said range should be wider than we’d like it to be for Sirlin’s balance standards, so the model isn’t a priori dismissing the possibility that it’s not balanced as we hope. It should be surprising, but not impossible. I need to sit down and think through this first, because my intuition for what sort of range to have isn’t very good at the moment.
Another aspect to the prior is that I might just be underestimating the spead in player skills, which would make the model increase the posterior deck strength spread to compensate. Given I’m only using tournament games at the moment, I was thinking player skill spread wouldn’t be as high as we’d expect from general players / casual games, but I could be way off-base in thinking that.
EDIT: To compare, there are just over 13,000 recorded tournament matches for Yomi right now, across 20 characters with no concept of turn-order, so 210 matchups. That’s about 62 matches per matchup, about 9 times the amount of data per matchup.
When I was running initial statistics, I dropped all the data from the top 3 and bottom 3 players, as otherwise their deck choices were dominating the results (ie Bashing went 9-1 in my data because I was the only person to use it, and mono-green did really badly because it had records of (approximately) 2-3, 3-3, 0-3, 0-3, 0-3 where the pile of 0-3 results were from players with few wins with any deck).
I didn’t have enough data points to run a baysean analysis, and tease out how much “better than personal average” spec choices made for each player.
Sounds reasonable. How many players was that with? Is that up on the forum somewhere?
I had it in a local spreadsheet where I was tracking tournament results (back when I was running the events). I didn’t have enough data to share, so it was just for my edification.
EricF’s old player rankings for the 2016 CASS series, which is longer ago than I’ve currently recorded, can be found here, if people want to compare.
I hadn’t taken a close look at your most recent post, @charnel_mouse, but it’s really awesome to see this project’s progress. This is a great contribution to the community
I wonder if there’d be any interest in a “peer review” games series, where we take the ten “least fair” matchups you listed in here, and try out playing ten games of just that matchup with a few different players at the helm of each. I agree with @Persephone that some of those matchups don’t jump out at me as intuitively lopsided.
I will say, I think your player skill model is honing in pretty well. Seems like a decent rank order w/ according confidence intervals.
Thanks, @FrozenStorm! Yeah, some of those matchups look far too lopsided, don’t they? I’m a bit happier with their general directions now, though.
I’d be pretty happy if there was some sort of “peer review” series. Sort of a targeted MMM? I’d be up for running / helping out with that.
I had been vaguely thinking of a setup where I take some willing players and give them decks that the model thinks would result in an even matchup, or matchups the model was least certain about. However, I was thinking of doing this over all legal decks, not just monocolour. In the model’s current state, this would probably result in so many lopsided matches that I didn’t think it would be fair to the players.
A quick update on the changes after CAMS19.
bansa jumps up the board after coming second with a Blue starter. Persephone enters on the higher end of the board after a strong performance with MonoGreen (I have no match data yet from before her hiatus).
Monocolour matchup details
| P1 deck | P2 deck | P1 win probability | matchup | fairness | |
|---|---|---|---|---|---|
| 1 | Green | Purple | 0.493 | 4.9-5.1 | 0.99 |
| 2 | Black | Black | 0.519 | 5.2-4.8 | 0.96 |
| 3 | Black | Purple | 0.481 | 4.8-5.2 | 0.96 |
| 4 | Green | Red | 0.519 | 5.2-4.8 | 0.96 |
| 5 | Blue | Blue | 0.473 | 4.7-5.3 | 0.95 |
| 6 | Blue | Purple | 0.473 | 4.7-5.3 | 0.95 |
| 7 | White | Blue | 0.461 | 4.6-5.4 | 0.92 |
| 8 | Purple | Purple | 0.548 | 5.5-4.5 | 0.90 |
| 9 | White | Black | 0.439 | 4.4-5.6 | 0.88 |
| 10 | Blue | Red | 0.569 | 5.7-4.3 | 0.86 |
| 11 | Green | Green | 0.431 | 4.3-5.7 | 0.86 |
| 12 | Red | Black | 0.572 | 5.7-4.3 | 0.86 |
| 13 | Green | White | 0.581 | 5.8-4.2 | 0.84 |
| 14 | Red | White | 0.409 | 4.1-5.9 | 0.82 |
| 15 | White | White | 0.591 | 5.9-4.1 | 0.82 |
| 16 | Red | Green | 0.610 | 6.1-3.9 | 0.78 |
| 17 | Red | Blue | 0.615 | 6.1-3.9 | 0.77 |
| 18 | Red | Red | 0.620 | 6.2-3.8 | 0.76 |
| 19 | Blue | Green | 0.627 | 6.3-3.7 | 0.75 |
| 20 | Blue | White | 0.630 | 6.3-3.7 | 0.74 |
| 21 | Purple | Red | 0.367 | 3.7-6.3 | 0.73 |
| 22 | White | Red | 0.655 | 6.6-3.4 | 0.69 |
| 23 | Black | Red | 0.663 | 6.6-3.4 | 0.67 |
| 24 | Purple | Black | 0.323 | 3.2-6.8 | 0.65 |
| 25 | Black | Blue | 0.693 | 6.9-3.1 | 0.61 |
| 26 | Purple | Blue | 0.300 | 3.0-7.0 | 0.60 |
| 27 | Black | White | 0.709 | 7.1-2.9 | 0.58 |
| 28 | Blue | Black | 0.289 | 2.9-7.1 | 0.58 |
| 29 | White | Purple | 0.264 | 2.6-7.4 | 0.53 |
| 30 | Green | Black | 0.262 | 2.6-7.4 | 0.52 |
| 31 | Black | Green | 0.745 | 7.5-2.5 | 0.51 |
| 32 | White | Green | 0.743 | 7.4-2.6 | 0.51 |
| 33 | Green | Blue | 0.753 | 7.5-2.5 | 0.49 |
| 34 | Purple | Green | 0.240 | 2.4-7.6 | 0.48 |
| 35 | Red | Purple | 0.801 | 8.0-2.0 | 0.40 |
| 36 | Purple | White | 0.824 | 8.2-1.8 | 0.35 |
The main difference here is that P1 MonoPurple is considered to take a beating from P2 MonoGreen (2.4-7.6). This is because the matchup didn’t have much evidence before, and CAMS19 had the following relevant matches:
- Unity [Balance/Growth]/Present vs. Legion [Anarchy]/Growth/Strength, Legion wins
- FrozenStorm [Future/Past]/Finesse vs. Unity [Balance/Growth]/Present, Unity wins
- Unity [Balance/Growth]/Present vs. Persephone MonoGreen, Persephone wins
- FrozenStorm [Future/Past]/Finesse vs. charnel_mouse [Balance]/Blood/Strength, charnel_mouse wins
All P2 wins.
Current monocolour Nash equilibrium:
P1: Pick Black or Red at 16:19.
P2: Pick Black or White at 6:1.
Value: About 5.5-4.5, slightly P1-favoured.
Slight change in overall matchup, both players favour Black much less than before.
If the turn order is unknown, then both players have the same equilibrium strategy: pick Black, all the time, since it outperforms all the other monodecks when averaged over turn order.
Next update should be for Metalize’s data.
I’m confused… these aren’t monocolor matchups, so why are they being considered for those monocolor probabilities? They indicate something about the starter choice, perhaps, but certainly not monocolor matchups…
Because the strength of a deck against another is modelled as the sum of 16 strength components:
- P1 starter vs. P2 starter (1 component, e.g. Green vs. Red)
- P1 starter vs. P2 specs (3 components, e.g. Green vs. Anarchy, Green vs. Growth, and Green vs. Strength)
- P1 specs vs. P2 starter (3 components, e.g. Balance vs. Red, Growth vs. Red, Present vs. Red)
- P2 specs vs. P2 specs (9 components I won’t list here, but which include Present vs. Growth for the first match)
For the example first match, only the Present vs. Growth component is relevant to the MonoPurple vs. MonoGreen matchup, but the second match has nine relevant components: any of Purple starter, Future spec, Past spec, vs. any of Green starter, Balance spec, Growth spec.
This allows a starter/spec’s performance in a deck to also inform its likely performance in other decks. I think this is reasonable, and if we don’t do this, the amount of information on most decks, including monodecks, is miniscule.
I originally introduced this approach here, albeit not in much detail:
I think Frozen is reasonably concerned that, without looking at the inner workings of the actual match, its a bit of a stretch to say present and growth actually faced off in any meaningful way. That said, such analysis of the inner workings of a match are well beyond the scope of this data compilation.
In a game where crashbarrows won the day, and the opponent was actively using strength, the fact that growth was an alternate option doesn’t directly mean growth is weak against crashbarrows, but taken together with player skill factors, the more skilled players will choose what they think is the best strategy vs a given deck and it will all even out in the long run.
In any event, I think the statistics are still informative.