More Yomi Data

[vengefulpickle]

I was inspired by @charnel_mouse’s analysis of the recent Codex tournament, and with some very helpful pointers from him, ran a similar analysis on all of our historical Yomi matches. My goal was to compute estimates of matchup numbers, taking into account all games played between the characters, and the skills of the players playing them.

To that end, I modeled the results of the matches using log odds of victory based on the difference in player skill plus the advantage for the first player based on the matchup. The player skill was computed per-tournament (but considered constant within a tournament), and was allowed to vary by a learned parameter between tournaments.

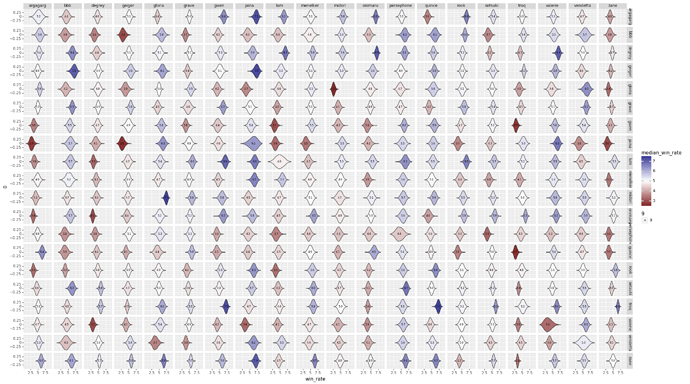
First, the matchup chart:

As usual, the rows are player 1, and the columns are player 2, so a box that is very blue favors the character labeled at the end of the row. Plots that are narrower indicate a higher confidence in the matchup number (due to either less variance in the matchup, more games played, or both).

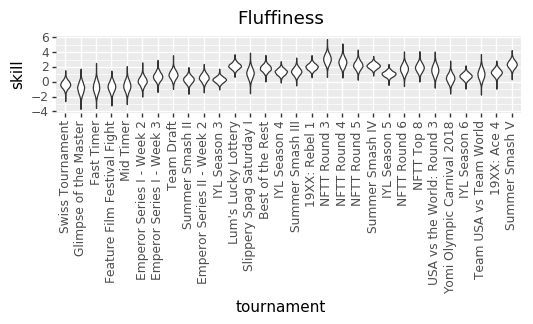
For skills, I don’t have a concise chart with everyone, but I’ll put a few examples so that you can see that the model learned something about player skill.

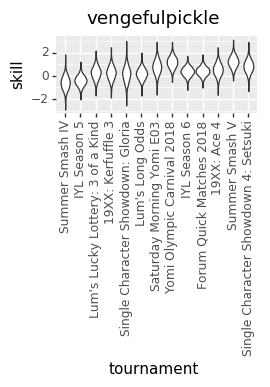
First, me!

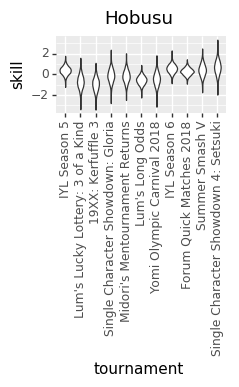
Then, the peoples champion, @mysticjuicer!

And finally, the storied career of the esteemed @cpat

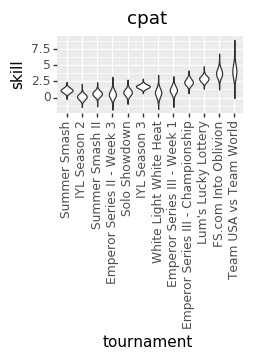
For reference on what those numbers mean, here’s a chart that @charnel_mouse through together when explaining the math to me:

Matchup	Difference in Log odds
1-9	-2.20
2-8	-1.39
3-7	-0.85
4-6	-0.41
5-5	0.00
6-4	0.41
7-3	0.85
8-2	1.39
9-1	2.20

So when you see @cpat clocking in at ~3.5 in his later tournaments, you can see just how far ahead he is over your average bear/new Yomi player.

[Hobusu]

you sorted the characters alphabetically, you monster

This is really cool! …But it’s also a bit overwhelming, so are there any notable results that could be highlighted?

[Fluffiness]

Perse with only 3 positive MUs. I cri evrytime.

[vengefulpickle]

A notable thing to my -loving heart was that this chart seems to run counter to the wisdom that she is a good counterpick to . Although, I suppose her matchup with him is at least better than the majority of the rest of her matchups…

I haven’t taken it back and compared it to some of my past work, to see how far off (say) the raw averages it is. Spot checking things:

MU	All-time Average	Estimated
-	5.2-4.8	5.1-4.9
-	5.8-4.2	5.3-4.7
-	3.8-6.2	3.4-6.6
-	4.7-5.3	4.5-5.5
-	4.2-5.8	4.2-5.8
-	4.4-5.6	5.2-4.8
-	4.9-5.1	5.1-4.9

also comes out of this looking pretty good (mostly positive across the whole cast). This is mostly in line with the global averages, except his and matchups.

[vengefulpickle]

Also, since you guys commented:

@Hobusu

@Fluffiness

[vengefulpickle]

Also, gross… I just looked at 's other counterpicks: , , and .

That’s pretty slim pickings. Both and have more to pick from.

[vengefulpickle]

And, looking at a particular tournament (in this case, IYL6)

Final results from IYL6:
1. CKR
2. MR75
3. Bomber678
3. Caralad
5. copper8642
5. FenixOfTheAshes
5. mysticjuicer
5. SouthpawHare
9. Fivec
9. JonnyD
9. sharpobject
9. snoc

EDIT: Someone stop me before I math again!

[Fluffiness]

To see that i’ve been gradually improving over the years makes me happy.

[Bryce_The_Rice]

If only lowtier hadn’t been dqd for never playing

[charnel_mouse]

Nice job @vengefulpickle, looks like you’ve far outpaced me at this point! How did you handle skill progression over time in the end?

[thehug0naut]

Really loving the stats based approach to matchup numbers. Great work to @charnel_mouse and @vengefulpickle for putting in the work for our beloved games. While I haven’t exhuastively gone through consensus lopsided matchups, a few key ones (, ) seem to be emerging as expected from the data, which is encouraging.

However I can see some of the mirror matches have numbers quite different from 5.0 - the worst at either end are (6.2) and (3.4). My first reaction was that these cases have pretty broad distributions indicating high variation, so I expect wide confidence intervals with no statistically significant deviation from 5.0. Part of me thinks that this could be ok, but we probably have to discount any result in with similar levels of variation since it can be as wrong as a true 5:5 being a 6:4 or 6.5:3.5.

But the more I think about it, the more its still bothering me. Surely the central value of mirror matches shouldn’t tend far from 5.0 given that every loss of Jaina vs Jaina is by definition also a win for Jaina vs Jaina. It makes me wonder if the model is placing some significance on P1 vs P2 which is relevant for codex but meaningless in Yomi.

@vengefulpickle can you confirm how P1 vs P2 is handled by the model and why these central values would deviate so much from their definitional value? (Yes I am asking for more math )

[Bryce_The_Rice]

At a guess, it’s weighting player skill within mirror matches heavily enough that it’s skewing the data. An interesting point, to be sure.

[vengefulpickle]

Yeah, I think the issue is a combination of the data with my current model. In particular, I don’t do anything to force mirror matches to be 5-5 with unknown variance, which means that if we don’t have a lot of instances of those games, then the randomness in the data about which player is coded as player 1 will distort the numbers. (For reference, I’m only actually calculating the MU numbers for the top half of the square, and then I’m mirroring them to the bottom.)

Here’s the model I’m using right now:

data {
    int<lower=0> NPT; // Number of player/tournaments
    int<lower=0> NG; // Number of games
    int<lower=0> NM; // Number of matchups
    int<lower=0, upper=1> win[NG]; // Did player 1 win game
    int<lower=1, upper=NPT> pt1[NG]; // Player/tournament 1 in game
    int<lower=1, upper=NPT> pt2[NG]; // Player/tournament 2 in game
    int<lower=1, upper=NM> mup[NG]; // Matchup in game
    int<lower=0, upper=NPT> prev_tournament[NPT]; // Previous tournament for player/tournament
}
parameters {
    vector[NPT] skill_adjust; // Skill change before player/tournament
    vector[NM] mu; // Matchup number
}
transformed parameters {
    vector[NPT] skill;
    
    for (t in 1:NPT) {
        if (prev_tournament[t] == 0)
            skill[t] = skill_adjust[t];
        else
            skill[t] = skill[prev_tournament[t]] + skill_adjust[t];
    }
    
}
model {
    skill_adjust ~ normal(0, 1);
    mu ~ normal(0, 1);
    win ~ bernoulli_logit(skill[pt1] - skill[pt2] + mu[mup]);
}

@charnel_mouse

How did you handle skill progression over time in the end?

I ended up making each player/tournament skill level a parameter to solve for. The raw parameters were actually the skill adjustment before each tournament, and then I passed in data to chain those adjustments together over time to compute the per-tournament skill.

[charnel_mouse]

@vengefulpickle

In particular, I don’t do anything to force mirror matches to be 5-5 with unknown variance, which means that if we don’t have a lot of instances of those games, then the randomness in the data about which player is coded as player 1 will distort the numbers.

I think Yomi mirror matchups should always be 5-5 once you remove player effects, so their prior variance should be considered as known to be zero. Then mirror matchup results give all their information to player skills.

[vengefulpickle]

As I’ve been thinking about the mirror-match problem, I realized that I’m not actually accounting for match variance correctly, either. The width in the chart above as actually only capturing the uncertainty in the model of the exact MU number. It doesn’t (as I originally thought) capture the natural variance in a Yomi game. Instead, I should be modeling the MU value and the MU variance as separate numbers, and adding a random effect based on the variance in my calculation for every game.

I’ll update this thread when I’ve accounted for that, and then we can talk about what the most swingy matchups are. =)

[mysticjuicer]

Also note, if it’s an artifact of P1 vs P2, that I tend to record the results in P1 to P2 order, where P1 is typically the reporting player, and also the winner about 90% of the time.

[vengefulpickle]

Yeah, I manually flipped half of the mirror matches around, to counter that effect. However, I think fixing the model will improve the situation.

For the other matchups, I flip the game around to have the earlier character (alphabetically) first, so there shouldn’t be any P1 effects there.

[vengefulpickle]

So, here’s a thing… Not sure what to make of it, honestly.

I factored out the standard deviation of the per-matchup variance, and graphed it up separately. Here’s the adjusted matchup chart, plus the standard devs.

Things that are odd: most of the std devs are basically 0.4… Except mirror matches which are ~0.2?

The Model

data {
    int<lower=0> NPT; // Number of player/tournaments
    int<lower=0> NG; // Number of games
    int<lower=0> NMG; // Number of mirror-games
    int<lower=0> NM; // Number of non-mirror matchups
    int<lower=0> NMM; // Number of mirror matchups
    
    int<lower=0, upper=NPT> prev_tournament[NPT]; // Previous tournament for player/tournament
    
    int<lower=0, upper=1> win[NG]; // Did player 1 win game
    int<lower=1, upper=NPT> pt1[NG]; // Player/tournament 1 in game
    int<lower=1, upper=NPT> pt2[NG]; // Player/tournament 2 in game
    int<lower=1, upper=NM> mup[NG]; // Matchup in game
    
    int<lower=0, upper=1> m_win[NMG]; // Did player 1 win mirror-match
    int<lower=1, upper=NPT> m_pt1[NMG]; // Player/tournament 1 in mirror-match
    int<lower=1, upper=NPT> m_pt2[NMG]; // Player/tournament 2 in mirror-match
    int<lower=1, upper=NM> m_mup[NMG]; // Matchup in mirror-match
    
}
parameters {
    vector[NPT] skill_adjust; // Skill change before player/tournament
    vector[NM] mu; // Matchup value
    vector<lower=0>[NM] muv; // Matchup variance
    vector<lower=0>[NMM] mmv; // Mirror-matchup variance
}
transformed parameters {
    vector[NPT] skill;
    
    for (t in 1:NPT) {
        if (prev_tournament[t] == 0)
            skill[t] = skill_adjust[t];
        else
            skill[t] = skill[prev_tournament[t]] + skill_adjust[t];
    }
    
}
model {
    vector[NG] g_v_raw;
    vector[NMG] mg_v_raw;
    
    g_v_raw = rep_vector(0, NG);
    mg_v_raw = rep_vector(0, NMG);

    skill_adjust ~ std_normal();
    mu ~ normal(0, 0.5);
    muv ~ normal(0, 0.25);
    mmv ~ normal(0, 0.1);
    
    g_v_raw ~ std_normal();
    mg_v_raw ~ std_normal(); 
    
    win ~ bernoulli_logit(skill[pt1] - skill[pt2] + mu[mup] + g_v_raw .* muv[mup]);
    m_win ~ bernoulli_logit(skill[m_pt1] - skill[m_pt2] + mg_v_raw .* mmv[m_mup]);
}

[mysticjuicer]

I honestly don’t folllow what any of these graphs mean. You’re going to have to break things waaaaay down for me to follow any of this.

[vengefulpickle]

Hah, fair enough. Don’t have time to do a writeup now, but I’ll work on one.