More Yomi Data

[vengefulpickle]

Ok, lemme try and break this down.

The Setup

Let’s say we’re talking about a specific game, say between myself and @mysticjuicer. If we had perfect information, we might be able to say that I’ll win with some probability p. Conversely, juicer will win with probability 1-p. Because we know something about Yomi, we could say that p probably depends on my skill, juicer’s skill, the difficulty of the particular character matchup, plus some randomness based on the luck of the draw that particular game. The goal of this exercise is to figure out what each of those skills is, what the actual much number is, and approximately how impactful the randomness of the deck is.

So, we have something like:

p ~= skill(pickle) - skill(juicer) + matchup(pers, troq) + variance(pers, troq)

In order to make the math more tractible, we’ll instead use the formula:

ln(p/1-p) = skill(pickle) - skill(juicer) + matchup(pers, troq) + variance(pers, troq)

That natural log ln is what I was talking about earlier with the table of Difference of Log Odds.

The Analysis

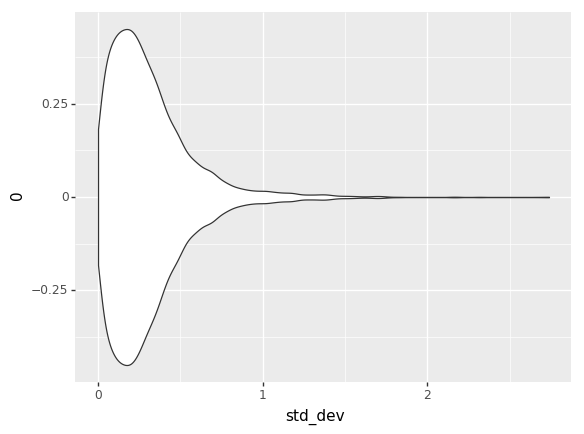
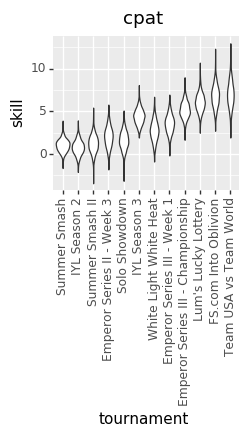
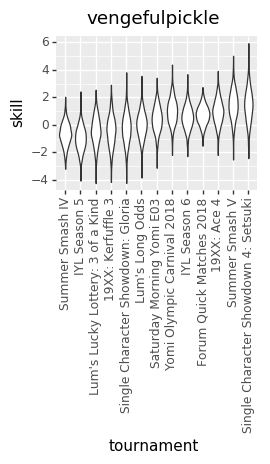
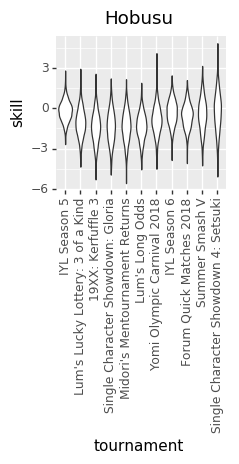
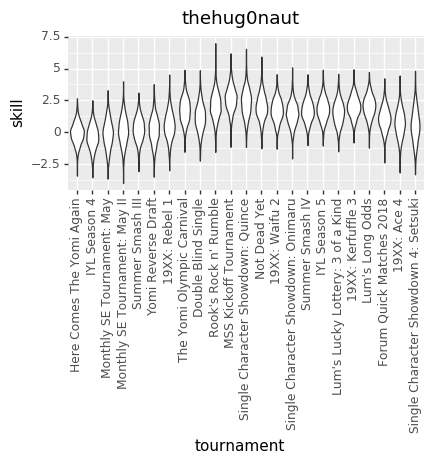
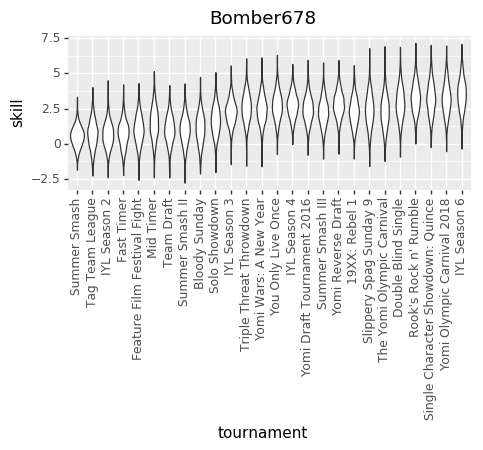
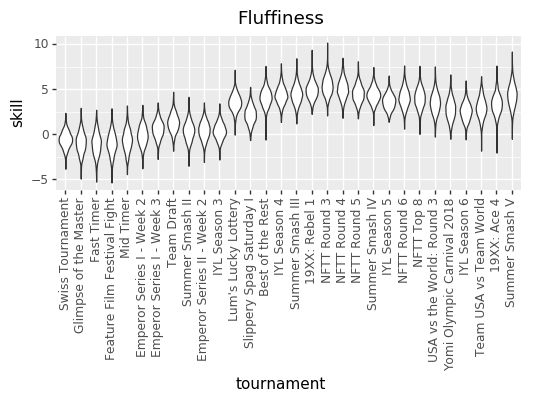
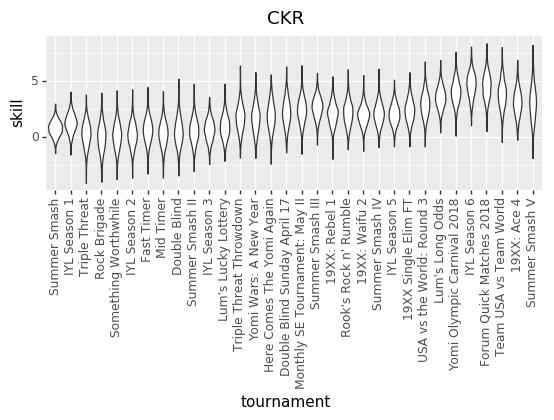
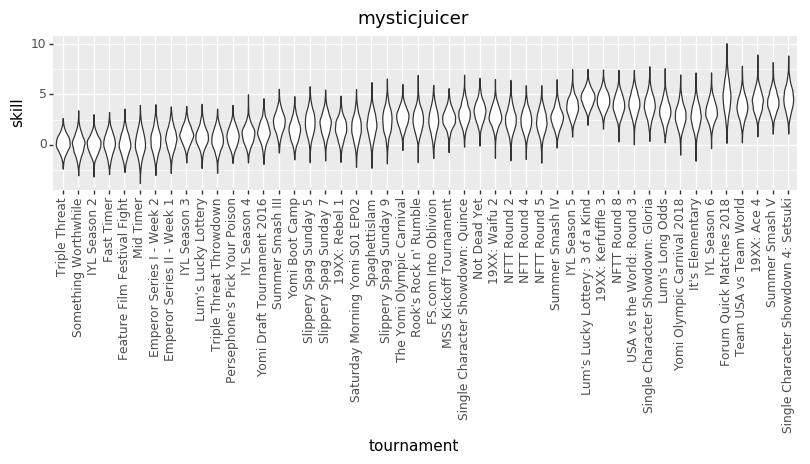
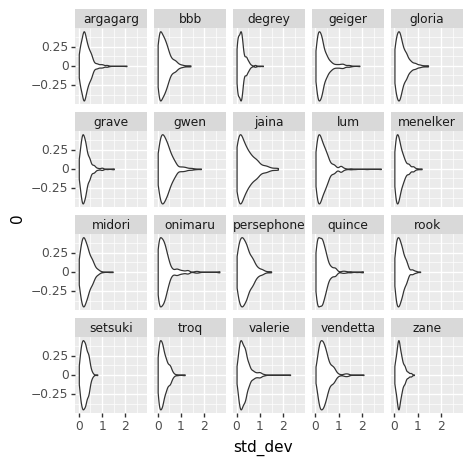
Because we don’t know the exact numbers, what we’re trying to do is estimate all of the skills (at points in time, across all players), matchup numbers, and variance amounts, by figuring out what values of those things best explain the actual outcomes we’ve seen in the Yomi historical data. We do that by basically taking a guess at all those parameters, seeing how well they explain the data, and then adjusting our guess at the parameters. Do that several thousand times and you end up with a bunch of parameter guesses. The graphs are charts of the number of times that we guessed each value for each parameter. The number in the middle of each graph is the median guess.

EDIT: The other relevant thing is that I converted The numbers in both charts out of log-odds space. That means, though, that each chart treats the other factors as irrelevant. That particularly affects the variance chart, where the same size variance in log-odds space will have different size effects on p based on (say) the matchup skew.

[snoc]

@vengefulpickle

we could say that p probably depends on my skill, juicer’s skill, the difficulty of the particular character matchup, plus some randomness based on the luck of the draw that particular game

I’m confused; it’s a long time since I did any stats, but doesn’t the fact that we are modelling things probabilistically mean that the variance of the draws in a given game shouldn’t be part of p? What’s left to be random other than those variables?

[vengefulpickle]

Hrm… The way I was thinking through it was that if we had perfect information, we would know exactly what the skill numbers were and the matchup number was, and that if those were fixed quantities, then we needed some other bit of randomness to “explain” p. But now that you’ve asked that question, I have to say I’m not entirely sure…

I ended up adding the extra factor for variance because I couldn’t figure out how to otherwise account for the variance in mirror matchups. But as I think through the question “What should p when playing a mirror match between equally skilled players”, then answer I come to is pretty clearly “Exactly 0.5”. Which argues, as you’re saying, for removing the extra fudge factor.

So, expect another updated chart, once my machine crunches all of the numbers again.

[vengefulpickle]

Perhaps there’s an argument for complicating the model by saying that there is a matchup-specific scaling factor on the skill difference? So, certain matches amplify skill differences more than others? I’m not sure how best to evaluate how accurate one model is over another, though.

[charnel_mouse]

It depends, I think, on when you’d expect skill to matter more. If it’s a matter of skill difference having a greater effect in closer matchups, then modelling skill difference as a linear effect on the log odds already does this. You can see this by looking at that log-odds vs. win probability table in the first post: changing the log odds has a greater effect on the probability near the 50/50 mark than it does at the extremes.

[vengefulpickle]

I think my theory is that some matchups are more luck-based than others (not that I have enough experience to back that up, but I feel like I’ve heard things to that effect in discussions). If that were true, then it seems like there should be some kind of matchup specific weighing to the skill effect. Not sure if a multiplicative scale is the right thing, though.

[charnel_mouse]

A multiplicative scale means you don’t have to worry about the sign of the skill difference, so it seems like a reasonable starting point for checking which matchups are affected.

[CKR]

@vengefulpickle , would you please give me one of those cool personalized charts? I would like to see if I have made any progress, or if I am just spinning my wheels. Thanks. Happy holidays!

[Bryce_The_Rice]

Yes please me too

[mysticjuicer]

You can always check your historical ELO too, fellas.

[CKR]

Yeah, I have done that. The lines should be similar, but I am still curious.

[vengefulpickle]

Yeah, can do. I’m away from my dev machine, but I’ve got variance charts waiting for me when I get back, and I’ll bang out a few more skill histories as well.

[thehug0naut]

I don’t know if this is helpful or not but the central value of standard deviations of mirror matches (0.16-0.17) is approximately the square of the non-mirror standard deviations (0.40-0.41).

I feel like maybe I should be able to spin a yarn about what this means in terms of the model but to be honest I just thought it was interesting. However if this observation helps tweak the model in the right direction I reserve the right to come back and make this post look smarter

[vengefulpickle]

I got a version of the model working that accounts for varying effects due to skill based on matchups. I’m not sure what to make of it yet, but here’s the charts.

Matchup

This is basically the same format as previous charts, and the numbers look similar (by eyeball, anyway)

Skill Effect Modifier

This chart is measuring the scaling factor that is applied to the difference in player skills. This factor varies per matchup. A value of 1 would mean that the skill difference affects the odds as described in my earlier explanatory post. A value less than 1 decreases the effect of a skill gap, and a value greater than 1 increases the effect of the skill gap.

My interpretation is that a matchup with a low skill multiplier is one that has high variance in play, and vice versa.

Top 10 Highest Variance MUs

Char 1	Char 2	Median Skill Multiplier
onimaru	zane	0.038801
quince	quince	0.051072
grave	onimaru	0.055356
degrey	quince	0.062899
bbb	bbb	0.063510
lum	menelker	0.064327
bbb	troq	0.064415
onimaru	rook	0.064824
persephone	persephone	0.076867
gwen	onimaru	0.081619

Top 10 Lowest Variance Matchups

Char 1	Char 2	Median Skill Effect
geiger	gloria	0.659470
onimaru	persephone	0.664453
grave	jaina	0.678687
geiger	jaina	0.683435
bbb	valerie	0.699217
vendetta	vendetta	0.780808
gwen	jaina	0.801282
argagarg	persephone	0.880664
jaina	quince	0.912223
lum	onimaru	1.238238

One thing that seems odd to me in this is that overall, most matches have the skill effects scaled down. Overall all matches, the distribution is:

And here are some updated individual skill charts. The biggest change, I think, is that the model is less certain about players’ skills in each tournament.

cpat

vengefulpickle

Hobusu

thehug0naut

Bomber678

Fluffiness

CKR

mysticjuicer

[vengefulpickle]

And, for grins, here’s the aggregate skill effect for each character

[mysticjuicer]

What does high or low variance mean in this model? Without referencing player skill, ideally.

[charnel_mouse]

I believe low-variance means that the result depends less on luck during the match, so player skill differences have more effect.

[vengefulpickle]

Yeah, exactly. My theory was: variance (in current Yomi parlance) means randomness/unpredictability of the matchup, which in turn would suggest that skill would have less of an influence on the match result, overall.

[mysticjuicer]

Maybe I’m still not understanding how to read the chart. I just looked at Lum vs Oni, which has the highest skill effect, and therefore is considered the lowest variance (?) but the distribution of the MU results is really wide? Is that because the skill effect is so significant?

Basically, what is being most measured and what is being interpreted in the chart? Is it measuring variance and we’re interpreting something about the skill effect, or is it measuring skill and we’re interpreting variance of the MU? Or both?

I’m looking at Rook vs BBB, and Rook vs Arg in the chart, and those look really good to me, based on my personal views of the MUs. I would describe both of those MUs as low-variance, and with low skill effects. I would expect a very inexperienced BBB or Arg player to learn those MUs over the course of a first to 4, for example, even against an amazing Rook player. Is that something that this model assumes is possible, or is low skill effect always defined by high variance?

[vengefulpickle]

Another avenue I’m curious about (but I’m not sure I have enough data to support) is what the model would look like if I took per-character skill into account. That would result in a lot more parameters, though, and might mean that the model would just overfit. We might be in elephant territory.