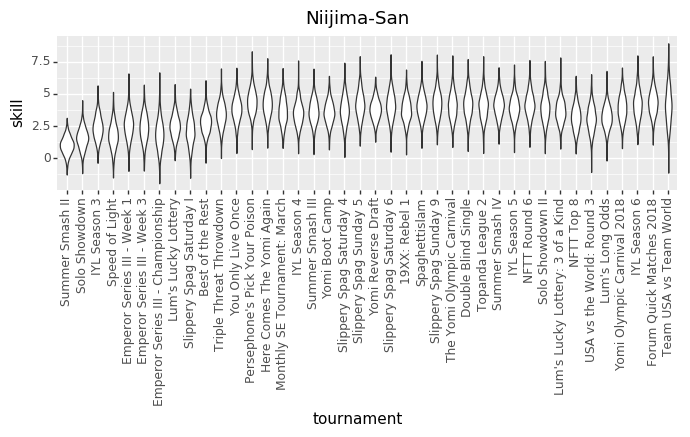
Yeah, I think at this point it’s worth setting something up in Stan so you can compare the model’s matchup predictions to what actually happens. That way you can see where the model’s doing well or needs improvements, and use that to inform adding more effects to it.
So, the things being measured by the model are: player skill per-tournament, matchup lopsided-ness, and a per-matchup multiplier that is applied to the skill difference when computing the log-odds.
The first two things have fairly straightforward interpretations. The multiplier is harder to interpret, honestly. Your Rook-Arg and Rook-BBB analysis suggests that perhaps skill-effect is just skill-effect, and that perhaps it’s due to randomness, or perhaps it’s due to it being a low-skill matchup, and the model can’t distinguish those cases.
I think a missing piece of data in these charts is how many games in that matchup we’ve seen (and perhaps also what the effective skill differences/absolute skill values were). Its possible that this MU is anomalous simply because it hasn’t been played very much.
Yeah, that would be excellent. I don’t actually know enough Stan to know what to look for, for that. Would those be generated quantities? I wanted to look at R-squared on a per-matchup basis, to use that to assess how well the model is fitting reality across the various matchups, but I’m not sure if that’s the right tool to use (I only really know enough stats to fake it).
As far as I can tell, yes, you’d be using generated quantities. I’ll PM you over some stuff.
Oh, and  John Cook.
John Cook.
So, I haven’t quite gotten to generating matches to see how well the parameters fit… but I was trying to figure out whether the weirdness in Oni/Lum was due to lack of data or something else, so I now have charts that estimate the number of games played in each matchup at each skill level (taking into account the model uncertainty in player skill level), and also the relative matchup score (also taking into account skill levels).
Games Played by Skill Level
Matchup by Skill Level
EDIT:
To answer the Oni/Lum question: yeah, we really just don’t have much data there. Although we have even less data in the Jaina mirror match. @snoc, maybe that should be the next SCS?
Possibly - I prefer to keep it random so nobody can accuse me of any bias though!
I can’t say I actually follow any of this. What I would like to know though, is:
Can you show Vendetta’s matchups and/or aggregate skill modifiers with and without my specific data added to the pool? Also just for fun could you post one of those curve thingies for me?
And then explain all of these things to me because I’m looking at weird blobbies?
Thanks.
The way the process works, there’s no really good way to extract your data from the overall model learning. I could re-run the process without any of your data, but I think a better way would be to try and model player-skill on a per-character basis. However, before I make any more model changes, I want to add a technique that will tell me how good the model is at actually predicting results (and thus, how good it is in general).
I’ll post a timeline for you in a minute, once I have a chance to generate it.
This explanation is probably still the most relevant: More Yomi Data - #21 by vengefulpickle
I appreciate the explanation but I understand what it is trying to do, i just don’t quite understand how it is being represented. Like I get that it’s trying to model results based on matchup strength, player skill, and variance, but why does it look like a sperm that hit a brick wall?
Ah… All of the blobs are violin charts/probability density charts… Meaning, the numbers on the x-axis where they’re bigger is a place where the model thinks the true value is more likely to be.
I honestly wouldn’t put too much stock in the skill-effects charts up above (the sperm-against-a-wall charts). At this point, I’m not super confident that they actually represent anything meaningful (and I’m hoping once I get cross-validation up and running, I can refine the model to something more useful/predictive).
Looks about how I thought it would. I just went up to wherever I am *now and never got any better after that.
Well, I did some more crunching. I wasn’t able to get a model that included per-character skill to perform well (I think it just had too many variables for the amount of data we have). I ended up removing the matchup multiplier (it didn’t seem to be helping), and stuck with a model that kept incremental changes between tournaments. The final player skill numbers look lower than the charts I posted above, which I think reflects that most of the matchup multipliers that I removed were reducing the skill gaps.
The Latest Model
data {
int<lower=0> NPT; // Number of player/tournaments
int<lower=0> NG; // Number of games
int<lower=0> NM; // Number of matchups
int<lower=0, upper=NPT> prev_tournament[NPT]; // Previous tournament for player/tournament
int<lower=0, upper=1> win[NG]; // Did player 1 win game
int<lower=1, upper=NPT> pt1[NG]; // Player/tournament 1 in game
int<lower=1, upper=NPT> pt2[NG]; // Player/tournament 2 in game
int<lower=1, upper=NM> mup[NG]; // Matchup in game
vector<lower=0, upper=1>[NG] non_mirror; // Is this a mirror matchup: 0 = mirror
}
parameters {
vector[NPT] skill_adjust; // Skill change before player/tournament
vector[NM] mu; // Matchup value
real<lower=0> skill_adjust_variance;
}
transformed parameters {
vector[NPT] pooled_skill_adjust = skill_adjust * skill_adjust_variance;
vector[NPT] skill;
for (t in 1:NPT) {
if (prev_tournament[t] == 0)
skill[t] = skill_adjust[t];
else
skill[t] = skill[prev_tournament[t]] + pooled_skill_adjust[t];
}
}
model {
skill_adjust ~ std_normal();
mu ~ normal(0, 0.5);
skill_adjust_variance ~ std_normal();
win ~ bernoulli_logit((skill[pt1] - skill[pt2]) + non_mirror .* mu[mup]);
}
generated quantities{
vector[NG] log_lik;
vector[NG] win_hat;
for (n in 1:NG) {
log_lik[n] = bernoulli_logit_lpmf(win[n] | (skill[pt1[n]] - skill[pt2[n]]) + non_mirror[n] * mu[mup[n]]);
win_hat[n] = bernoulli_logit_rng((skill[pt1[n]] - skill[pt2[n]]) + non_mirror[n] * mu[mup[n]]);
}
}
Per-player charts to come once I can make them a little more legible.
I realized a couple of nights ago that I’ve been discarding a great source of data: the ELO numbers that I’m already calculating. So, I added that in, and that gave me enough data to get pretty good per-character skill levels for every player. However, that led to a much more opinionated matchup chart. I’m not sure if it’s good opinionated or just plain wrong, though. I’d love to hear your takes on whether this chart or the one above looks more correct (cc @mysticjuicer, @Niijima-san, @cpat)
Character Skill Levels
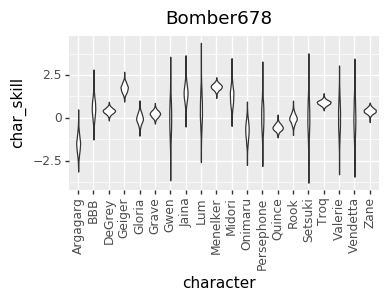
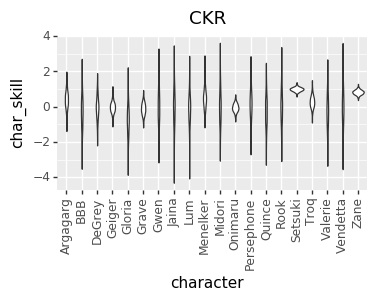
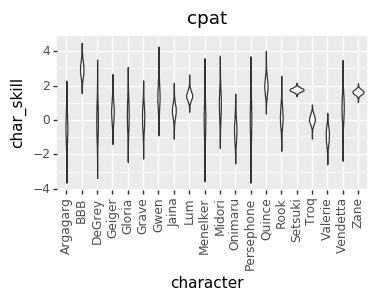
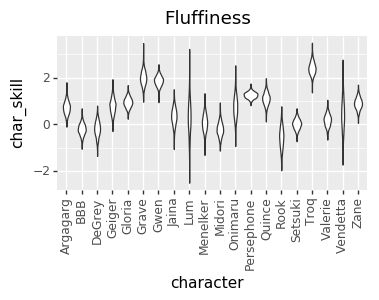
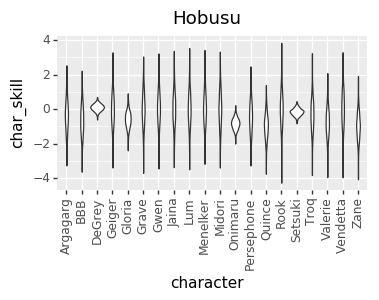
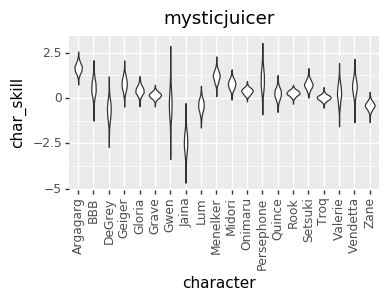
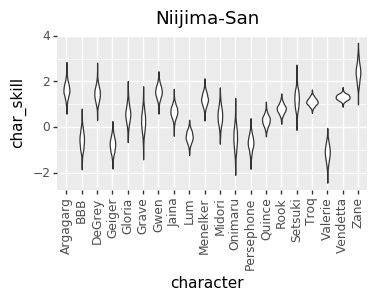
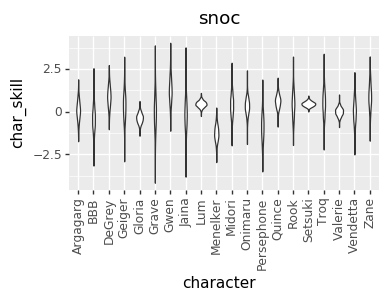
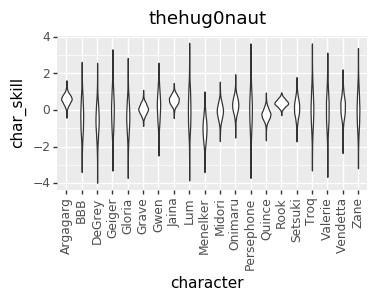
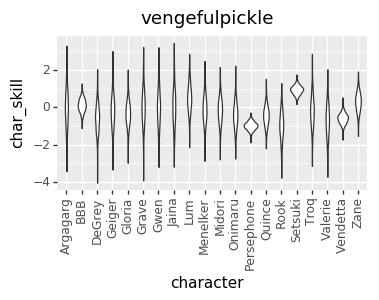
The Model
data {
int<lower=0> NG; // Number of games
int<lower=0> NM; // Number of matchups
int<lower=0> NP; // Number of players
int<lower=0> NC; // Number of characters
int<lower=0, upper=1> win[NG]; // Did player 1 win game
int<lower=1, upper=NM> mup[NG]; // Matchup in game
vector<lower=0, upper=1>[NG] non_mirror; // Is this a mirror matchup: 0 = mirror
int<lower=1, upper=NC> char1[NG]; // Character 1 in game
int<lower=1, upper=NC> char2[NG]; // Character 2 in game
int<lower=1, upper=NP> player1[NG]; // Player 1 in game
int<lower=1, upper=NP> player2[NG]; // Player 1 in game
vector[NG] elo_logit; // Player 1 ELO-based logit win chance
}
parameters {
vector[NM] mu; // Matchup value
vector[NP] char_skill[NC]; // Player skill at character
real elo_logit_scale; // elo_logit scale
}
transformed parameters {
vector[NG] player_char_skill1;
vector[NG] player_char_skill2;
vector[NG] win_chance_logit;
for (n in 1:NG) {
player_char_skill1[n] = char_skill[char1[n], player1[n]];
player_char_skill2[n] = char_skill[char2[n], player2[n]];
}
win_chance_logit = (player_char_skill1 - player_char_skill2) + non_mirror .* mu[mup] + elo_logit_scale * elo_logit;
}
model {
for (n in 1:NC) {
char_skill[n] ~ std_normal();
}
mu ~ normal(0, 0.5);
elo_logit_scale ~ std_normal();
win ~ bernoulli_logit(win_chance_logit);
}
generated quantities{
vector[NG] log_lik;
vector[NG] win_hat;
for (n in 1:NG) {
log_lik[n] = bernoulli_logit_lpmf(win[n] | win_chance_logit[n]);
win_hat[n] = bernoulli_logit_rng(win_chance_logit[n]);
}
}
Most Even Matchups
| Character | Counterpick |
|---|---|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
 |
     
|
Hmm.
I’m going to continue to assert that Arg vs Rook is one of Rook’s worst MUs, but I can understand how the historical chart wouldn’t bear that out. Arg vs Gloria being one of his most even MUs seems insane, but I could see how there wouldn’t be much argument to support too lopsided a number based purely on the historical results.
Grave vs Valerie being of his most even MUs seems odd - I’m pretty sure that’s a really good MU for Grave.
Oni vs Persephone is 5.7 to Oni in the historical chart; granted it’s over only 50ish games, but still, putting that as even seems like a reach. Same with Oni vs Menelker, which is 6.0 in the historical chart, over a larger set of games.
Troq vs Valerie is 6.5 to Troq in the historical chart, over like 150 games. Very odd to see it considered one of either characters most even MUs.
Zane vs Valerie is 5.8 to Zane in the historical chart, over 150 games as well. Definitely odd to see it listed as one of Zane’s most even MUs over Zane/Oni.
What breaks all this data is several things, but the biggest is probably the best players in the game having consistent CPs they use and always win with. Deluks used Troq against zane and went 20-5 in tournaments. If Deluks had to use Oni against Zane I would bet he would have been close to 20-5 and Oni-Zane MU wouldn’t look like what it was. The best players ever always used the same chars vs the same chars, and then worse players would use a pseudo-even distribution of everything else, making most of this data not actually useful I’m pretty sure. This really is just measuring who the bst players used for the most lopsided CP matches
Hmm… That’s an interesting point. I think my analysis should be able to compensate that at least some. In particular, if a particular player is dominant in a game (based on their know ELO), then the model should mostly assign responsibility to the skill differential, rather than to the matchup or character skill.
Also, if Deluks is 20-5 as Troq over Zane, and that includes matches against similarly skilled opponents, doesn’t that suggest that Troq is actually that dominant against Zane, at the top end?
That said, there are a couple different model tweaks I want to make that might make it more accurate. Also, I think that it can be good practice to weight multiple models and mix their results, so I want to see what that looks like.
I’m not actually sure the difference between the two charts. Is the second one with player skill compensated out, or in? For example in the first chart Gloria beats Vendetta handily, yet in the second chart Vendetta beats Gloria handily. Does this mean that if the players are average skill Vendetta wins and that the Gloria players were winning in skill alone, or vice versa, or something else entirely?
In the first chart, I was trying to impute player skill inside the model. It didn’t attempt to impute the skill of each player at particular characters.
The second chart uses to players relative Elo scores as a measure of their global skill, and then based on that tries to factor out the matchup rating and individual player skill at particular characters.
I think I’d need to dig in to the data to say more specifically why that particular matchup swapped. However, speculating a little, it could be that the first model was trying to stuff Gloria-specific skill into the global player skill, but there was other evidence that didn’t support that, and so it had to put those effects into the MU number instead.